The properties of the 6 trigonometric functions: sin (x), cos (x), tan(x), cot (x), sec (x) and csc (x) are discussed. These include the graph, domain, range, asymptotes (if any), symmetry, x and y intercepts and maximum and minimum points.

Sine Function : f(x) = sin (x)

• Graph
• Domain: all real numbers
• Range: [-1 , 1]
• Period = 2pi
• x intercepts: x = k pi , where k is an integer.
• y intercepts: y = 0
• maximum points: (pi/2 + 2 k pi , 1) , where k is an integer.
• minimum points: (3pi/2 + 2 k pi , -1) , where k is an integer.
• symmetry: since sin(-x) = - sin (x) then sin (x) is an odd function and its graph is symmetric with respect to the origin (0 , 0).
• intervals of increase/decrease: over one period and from 0 to 2pi, sin (x) is increasing on the intervals (0 , pi/2) and (3pi/2 , 2pi), and decreasing on the interval (pi/2 , 3pi/2).

Cosine Function : f(x) = cos (x)

• Graph
• Domain: all real numbers
• Range: [-1 , 1]
• Period = 2pi
• x intercepts: x = pi/2 + k pi , where k is an integer.
• y intercepts: y = 1
• maximum points: (2 k pi , 1) , where k is an integer.
• minimum points: (pi + 2 k pi , -1) , where k is an integer.
• symmetry: since cos(-x) = cos (x) then cos (x) is an even function and its graph is symmetric with respect to the y axis.
• intervals of increase/decrease: over one period and from 0 to 2pi, cos (x) is decreasing on (0 , pi) increasing on (pi , 2pi).

Tangent Function : f(x) = tan (x)

• Graph
• Domain: all real numbers except pi/2 + k pi, k is an integer.
• Range: all real numbers
• Period = pi
• x intercepts: x = k pi , where k is an integer.
• y intercepts: y = 0
• symmetry: since tan(-x) = - tan(x) then tan (x) is an odd function and its graph is symmetric with respect the origin.
• intervals of increase/decrease: over one period and from -pi/2 to pi/2, tan (x) is increasing.
• Vertical asymptotes: x = pi/2 + k pi, where k is an integer.

Cotangent Function : f(x) = cot (x)

• Graph
• Domain: all real numbers except k pi, k is an integer.
• Range: all real numbers
• Period = pi
• x intercepts: x = pi /2 + k pi , where k is an integer.
• symmetry: since cot(-x) = - cot(x) then cot (x) is an odd function and its graph is symmetric with respect the origin.
• intervals of increase/decrease: over one period and from 0 to pi, cot (x) is decreasing.
• Vertical asymptotes: x = k pi, where k is an integer.

Secant Function : f(x) = sec (x)

• Graph
• Domain: all real numbers except pi/2 + k pi, n is an integer.
• Range: (-infinity , -1] U [1 , +infinity)
• Period = 2 pi
• y intercepts: y = 1
• symmetry: since sec(-x) = sec (x) then sec (x) is an even function and its graph is symmetric with respect to the y axis.
• intervals of increase/decrease: over one period and from 0 to 2 pi, sec (x) is increasing on (0 , pi/2) U (pi/2 , pi) and decreasing on (pi , 3pi/2) U (3pi/2 , 2pi).
• Vertical asymptotes: x = pi/2 + k pi, where k is an integer.

Cosecant Function : f(x) = csc (x)

• Graph
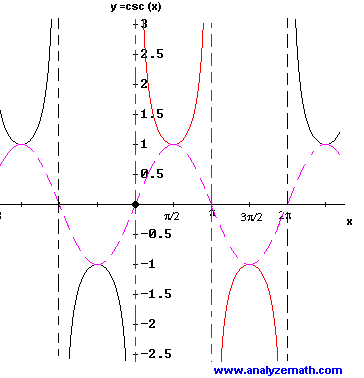
• Domain: all real numbers except k pi, k is an integer.
• Range: (-infinity , -1] U [1 , +infinity)
• Period = 2pi
• symmetry: since csc(-x) = - csc(x) then csc (x) is an odd function and its graph is symmetric with respect the origin.
• intervals of increase/decrease: over one period and from 0 to 2pi, csc (x) is decreasing on (0 , pi/2) U (3pi/2 , 2pi) and increasing on (pi/2 , pi) U (pi / , 3pi/2).
• Vertical asymptotes: x = k pi, where k is an integer.