Espacios vectoriales - Ejemplos con soluciones
Introducción a los espacios vectoriales
Consideremos las siguientes ecuaciones:
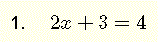 esta ecuación involucra sumas de expresiones reales y multiplicaciones por números reales
esta ecuación involucra sumas de expresiones reales y multiplicaciones por números reales
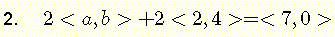 esta ecuación implica sumas de vectores bidimensionales y multiplicaciones por números reales
esta ecuación implica sumas de vectores bidimensionales y multiplicaciones por números reales
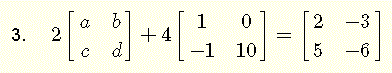 esta ecuación involucra sumas de matrices de 2 por 2 y multiplicaciones por números reales
esta ecuación involucra sumas de matrices de 2 por 2 y multiplicaciones por números reales
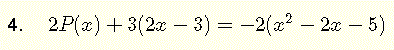 esta ecuación involucra sumas de polinomios y multiplicaciones por números reales.
esta ecuación involucra sumas de polinomios y multiplicaciones por números reales.
Es obvio que si el conjunto de números reales en la ecuación (1), el conjunto de vectores bidimensionales usados ??en la ecuación (2), el conjunto de matrices de 2 por 2 usados ??en la ecuación (3) y el conjunto de polinomios usados en la ecuación (4) obedecen algunas leyes comunes de la suma y la multiplicación por números reales, es posible que podamos resolver todas estas 4 ecuaciones y muchas otras preguntas más complicadas, usando el mismo algoritmo basado en las propiedades (o leyes) de la suma y multiplicación por números reales.
Clasificar conjuntos por sus propiedades ayuda a resolver problemas que involucran diferentes tipos de objetos matemáticos, como matrices, polinomios, vectores 2-d, vectores 3-d, vectores n-d, planos en geometría, funciones... y desarrollar formas y métodos para resolver diferentes problemas utilizando los mismos algoritmos.
Definición de un espacio vectorial
En lo que sigue, los espacios vectoriales (1 , 2) están en mayúsculas y sus elementos (llamados vectores) están en negrita minúsculas.
Un conjunto no vacío V cuyos vectores (o elementos) pueden combinarse usando las operaciones de suma (+) y multiplicación · por un escalar se llama un espacio vectorial si se cumplen las condiciones en A y B a continuación:
Nota Un elemento u objeto de un espacio vectorial se llama vector.
A) la adición de dos vectores cualquiera de V y la multiplicación de cualquier vector de V por un escalar produce un elemento que pertenece a V .
Sean u y v dos elementos cualesquiera del conjunto V y r cualquier número real.
\( \) \( \) \( \) \( \)
1) \( \textbf{u} + \textbf{v} = \textbf{w}\) , \( \textbf{w} \) es un elemento del conjunto \( V\) ; decimos que el conjunto \( V\) es cerrado bajo la suma de vectores
2)
\( r \cdot \textbf{u} = \textbf{z} \) , \( \textbf{z} \) es un elemento del conjunto \( V\) decimos que el conjunto \( V\) es cerrado bajo la multiplicación escalar
B) Para cualquier vector \( \textbf{u}, \textbf{v}, \textbf{w} \) en \( V\) y cualquier número real \( r \) y \( s \), las dos operaciones descritas anterior debe obedecer las siguientes reglas:
3) Conmutatividad de la suma de vectores: \( \textbf{u} + \textbf{v} = \textbf{v} + \textbf{u} \)
4) Asociatividad de la suma de vectores: \( (\textbf{u} + \textbf{v}) +\textbf{w} = \textbf{v} + ( \textbf{u} + \textbf{w}) \)
5) Asociatividad de la multiplicación: \( r \cdot (s \cdot \textbf{u}) = (r \cdot s) \cdot \textbf{u} \)
6) Un vector cero \( \textbf{0} \) existe en \( \textbf{v}\) y es tal que para cualquier elemento \( \textbf{u}\) en el conjunto \( \textbf{v }\), tenemos: \( \textbf{u} + \textbf{0} = \textbf{u} \)
7) Para cada vector \( \textbf{u}\) en \( V\) existe un vector \( - \textbf{u} \) en \( V\), llamado negativo de \( \textbf{ u}\), tal que: \( \textbf{u} + (- \textbf{u}) = \textbf{0} \)
8) Distributividad de Adición de Vectores: \( r \cdot (\textbf{u} + \textbf{v} ) = r \cdot \textbf{u} + r \cdot \textbf{v} \)
9) Distributividad de la Suma de Números Reales: \( (r + s) \cdot \textbf{u} = r \cdot \textbf{u} + s \cdot \textbf{u} \)
10) Para cualquier elemento \( \textbf{u}\) en \( V\) tenemos: \( 1 \cdot \textbf{u} = \textbf{u} \)
NOTAS
1) Aunque el elemento de un espacio vectorial se denomina vector, un espacio vectorial puede ser un conjunto de matrices, funciones, soluciones de ecuaciones diferenciales, vectores tridimensionales, ...., no tienen por qué ser VECTORES de n dimensiones como vectores de 2 o 3 dimensiones utilizados en física.
Ejemplos de espacios vectoriales
Ejemplo 1
Los siguientes son ejemplos de espacios vectoriales:
- El conjunto de todos los números reales \( \mathbb{R} \) asociados con la suma y la multiplicación escalar de números reales.
- El conjunto de todos los números complejos \( \mathbb{C} \) asociados con la suma y multiplicación escalar de números complejos.
- El conjunto de todos los polinomios \( R_n(x) \) con coeficientes reales asociados a la suma y multiplicación escalar de polinomios.
- El conjunto de todos los vectores de dimensión \( n \) escritos como \( \mathbb{R}^n \) asociados con la suma y la multiplicación escalar como se define para vectores de 3 y 2 dimensiones, por ejemplo.
- El conjunto de todas las matrices de dimensión \( m \times n \) asociado con la suma y la multiplicación escalar como se define para las matrices.
- El conjunto de todas las funciones \( \textbf{f} \) que satisfacen la ecuación diferencial \( \textbf{f} = \textbf{f '} \)
Ejemplo 2
Demuestre que el conjunto de todas las matrices de 2 por 2 asociadas con la suma de matrices y la multiplicación escalar de matrices es un espacio vectorial.
Solución al Ejemplo 2
Sea \( V\) el conjunto de todas las matrices de 2 por 2.
1) La suma de matrices da
\( \begin{bmatrix}
a & b \\
c & d
\end{bmatrix} +
\begin{bmatrix}
a' & b' \\
c' & d'
\end{bmatrix}
=
\begin{bmatrix}
a+a' & b+b' \\
c+c' & d+d'
\end{bmatrix}
\)
Sumar cualquier matriz de 2 por 2 da como resultado una matriz de 2 por 2 y, por lo tanto, el resultado de la suma pertenece a \( V \).
2) La multiplicación escalar de matrices da da
\( r \begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
=
\begin{bmatrix}
r a & r b \\
r c & r d
\end{bmatrix} \)
Multiplique cualquier matriz de 2 por 2 por un escalar y el resultado es una matriz de 2 por 2 que es un elemento de \( V \).
3) Conmutatividad
\( \begin{bmatrix}
a & b \\
c & d
\end{bmatrix} +
\begin{bmatrix}
a' & b' \\
c' & d'
\end{bmatrix}
\\\\
=
\begin{bmatrix}
a+a' & b+b' \\
c+c' & d+d'
\end{bmatrix}
\\\\ =
\begin{bmatrix}
a'+a & b'+b \\
c'+c & d'+d
\end{bmatrix}
\\\\ =
\begin{bmatrix}
a' & b' \\
c' & d'
\end{bmatrix} +
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\)
4) Asociatividad de la suma de vectores
\(
\left (
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix} +
\begin{bmatrix}
a' & b' \\
c' & d'
\end{bmatrix}
\right)
+
\begin{bmatrix}
a'' & b'' \\
c'' & d''
\end{bmatrix}
\\ =
\begin{bmatrix}
a+a' & b+b' \\
c+c' & d+d'
\end{bmatrix}
+
\begin{bmatrix}
a'' & b'' \\
c'' & d''
\end{bmatrix}
\\\\ =
\begin{bmatrix}
(a+a')+a'' & (b+b')+b'' \\
(c+c') + c''& (d+d')+d''
\end{bmatrix}
\\\\ =
\begin{bmatrix}
a+(a'+a'') & b+(b'+b'') \\
c+(c' + c'')& d+(d'+d'')
\end{bmatrix}
\\\\ =
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix} +
\left(
\begin{bmatrix}
a' & b' \\
c' & d'
\end{bmatrix}
+
\begin{bmatrix}
a'' & b'' \\
c'' & d''
\end{bmatrix}
\right)
\)
5) Asociatividad de la multiplicación
\(
r \left( s \begin{bmatrix}
a & b \\
c & d
\end{bmatrix} \right)
=
r \left( \begin{bmatrix}
s a & s b \\
s c & s d
\end{bmatrix} \right)
\\\\ =
\begin{bmatrix}
r s a & r s b \\
r s c & r s d
\end{bmatrix}
\\\\ =
\begin{bmatrix}
(r s) a & (r s) b \\
(r s) c & (r s) d
\end{bmatrix}
\\\\ =
(r s)
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\)
6) Vector cero
\( \begin{bmatrix}
a & b \\
c & d
\end{bmatrix} +
\begin{bmatrix}
0 & 0 \\
0 & 0
\end{bmatrix}
\\\\ =
\begin{bmatrix}
a+0 & b+0 \\
c+0 & d+0
\end{bmatrix}
=
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\)
7) vector negativo
\( \begin{bmatrix}
a & b \\
c & d
\end{bmatrix} +
\begin{bmatrix}
- a & - b \\
- c & - d
\end{bmatrix}
\\\\ =
\begin{bmatrix}
a+(-a) & b+(-b) \\
c+(-c) & d+(-d)
\end{bmatrix}
\\\\ =
\begin{bmatrix}
0 & 0 \\
0 & 0
\end{bmatrix}
\)
8) Distributividad de sumas de matrices:
\(
r
\left (
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix} +
\begin{bmatrix}
a' & b' \\
c' & d'
\end{bmatrix}
\right)
\\\\ =
\begin{bmatrix}
r(a+a') & r(b+b') \\
r(c+c') & r(d+d')
\end{bmatrix}
\\\\ =
\begin{bmatrix}
r a+ r a' & r b+ r b \\
r c+r c' & r d+ r d
\end{bmatrix}
\\\\ =
r \left (
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix} \right) + r \left(\begin{bmatrix}
a' & b' \\
c' & d'
\end{bmatrix} \right)
\)
9) Distributividad de sumas de números reales:
\(
(r + s ) \begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
=
\begin{bmatrix}
(r + s ) a & (r + s ) b \\
(r + s ) c & (r + s ) d
\end{bmatrix}
\\\\=
\begin{bmatrix}
r a + s a & r b + s b \\
r c + s c & r d + s d
\end{bmatrix}
\\\\=
\begin{bmatrix}
r a & r b \\
r c & r d
\end{bmatrix} + \begin{bmatrix}
s a & s b \\
s c & s d
\end{bmatrix}
\\\\=
r \begin{bmatrix}
a & b \\
c & d
\end{bmatrix} + s \begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\)
10) Multiplicación por 1.
\( 1 \begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
=
\begin{bmatrix}
1 a & 1 b \\
1 c & 1 d
\end{bmatrix}
=
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\)
Ejemplo 3
Muestre que el conjunto de todas las funciones reales continuas en \( (-\infty,\infty) \) asociadas con la suma de funciones y la multiplicación de matrices por un escalar forman un espacio vectorial.
Solución al Ejemplo 3
Del cálculo, sabemos si \( \textbf{f} \) y \( \textbf{g} \) son funciones continuas reales en \( (-\infty,\infty) \) y \( r \) es una número real entonces
\( (\textbf{f} + \textbf{g})(x) = \textbf{f}(x) + \textbf{g}(x) \) También es continua en \( (-\infty,\infty) \)
y
\( r \textbf{f}(x) \) también es continua en \( ( -\infty,\infty ) \)
Por lo tanto, el conjunto de funciones continuas en \( (-\infty,\infty) \) se cierra bajo suma y multiplicación escalar (las dos primeras condiciones anteriores).
Las 8 reglas restantes se cumplen automáticamente ya que las funciones son funciones reales.
Ejemplo 4
Demuestre que el conjunto de todos los polinomios reales con un grado \( n \le 3 \) asociado con la suma de polinomios y la multiplicación de polinomios por un escalar forman un espacio vectorial.
Solución al Ejemplo 4
La suma de dos polinomios de grado menor o igual a 3 es un polinomio de grado menor o igual a 3.
La multiplicación, de un polinomio de grado menor o igual a 3, por un número real da como resultado un polinomio de grado menor o igual a 3
Por lo tanto, el conjunto de polinomios de grado menor o igual a 3 se cierra bajo la suma y la multiplicación escalar (las dos primeras condiciones anteriores).
Las 8 reglas restantes se cumplen automáticamente ya que los polinomios son reales.
Ejemplo 5
Demuestre que el conjunto de polinomios con un grado \( n = 4 \) asociado con la suma de polinomios y la multiplicación de polinomios por un número real NO ES un espacio vectorial.
Solución al Ejemplo 5
La suma de dos polinomios de grado 4 puede no dar como resultado un polinomio de grado 4.
Ejemplo: Sea \( \textbf{P}(x) = -2 x^4+3x^2- 2x + 6 \) y \( \textbf{Q}(x) = 2 x^4 - 5x^2 + 10 \)
\( \textbf{P}(x) + \textbf{Q}(x) = (-2 x^4+3x^2- 2x + 6 ) + ( 2 x^4 - 5x^2 + 10) = - 5x^2 - 2 x + 16 \)
El resultado no es un polinomio de grado 4. Por lo tanto, el conjunto no es cerrado bajo la suma y, por lo tanto, NO es un espacio vectorial.
Ejemplo 6
Demuestre que el conjunto de enteros asociados con la suma y la multiplicación por un número real NO ES un espacio vectorial.
Solución al Ejemplo 6
La multiplicación de un número entero por un número real puede no ser un número entero.
Ejemplo: Sea \( x = - 2 \)
Si multiplicas \( x \) por el número real \( \sqrt 3 \) el resultado NO es un número entero.
Más referencias y enlaces
- Linear Algebra and its Applications - 5 th Edition - David C. Lay , Steven R. Lay , Judi J. McDonald
- Elementary Linear Algebra - 7 th Edition - Howard Anton and Chris Rorres
- Matrices with Examples and Questions with Solutions
- Polynomials
- Complex Numbers
Add, Subtract and Scalar Multiply Matrices
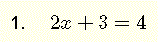 esta ecuación involucra sumas de expresiones reales y multiplicaciones por números reales
esta ecuación involucra sumas de expresiones reales y multiplicaciones por números reales
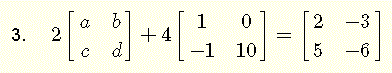 esta ecuación involucra sumas de matrices de 2 por 2 y multiplicaciones por números reales
esta ecuación involucra sumas de matrices de 2 por 2 y multiplicaciones por números reales
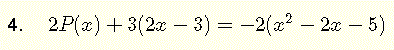 esta ecuación involucra sumas de polinomios y multiplicaciones por números reales.
esta ecuación involucra sumas de polinomios y multiplicaciones por números reales.