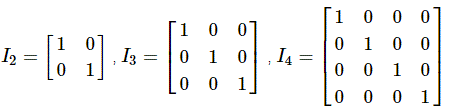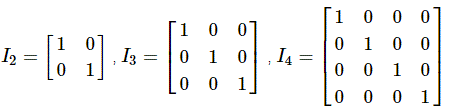Preguntas de matriz inversa con soluciones

Tutoriales que incluyen ejemplos y preguntas con soluciones detalladas sobre cómo encontrar el inverso del cuadrado matrices utilizando el método de la forma escalonada por filas y el método de los cofactores. Se analizan las propiedades de las matrices inversas y se incluyen varias preguntas, incluidas algunas desafiantes, relacionadas con las matrices inversas junto con sus soluciones detalladas.

Contenido de página

• Definición de la matriz de identidad
• Definición de la inversa de una matriz
• Encuentre la inversa de una matriz cuadrada utilizando el método de reducción por filas
• Encuentre el Inverso de una Matriz Cuadrada Usando Menores, Cofactores y Adjugado
• Fórmula para la inversa de una matriz de 2 por 2
• Propiedades de Matrices Inversas
• Preguntas sobre Matrices Inversas
• Soluciones a las preguntas
• Referencias

Definición de Matriz de identidad

La matriz identidad I _n es la matriz cuadrada con orden n x n y con los elementos en la diagonal principal que consisten en 1 y todos los demás elementos son iguales a cero .
Ejemplos de matrices de identidad

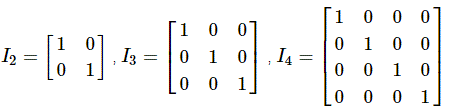
Definición de la inversa de una matriz

Sea A una matriz cuadrada de orden n x n. Si existe una matriz B del mismo orden tal que
A B = I _n = B A
donde I _n es la matriz identidad de orden n x n, entonces B se denomina matriz inversa de A y la matriz A es la matriz inversa de B.
Ejemplo 1
Verifique que las matrices A y B dadas a continuación son inversas entre sí.


Solución
Encontremos los productos AB y BA


AB = BA = I ₂ y por lo tanto A y B son inversas entre sí.
La inversa de una matriz cuadrada A se denota como A ^-1 y es única.

Encuentre la inversa de una matriz cuadrada utilizando el método de reducción por filas

Ejemplo 2
Encuentre la inversa de la matriz A dada por \[ A = \begin{bmatrix} 1&1 \\ 2&4 \end{bmatrix} \] si existiera..
Solución
Escribe la matriz aumentada \( [ A | I )\) \[ \begin{bmatrix} 1&1&|&1&0\\2&4&|&0&1 \end{bmatrix} \] paso 1 \[ \color{red}{\begin{matrix} \\ R_2 - 2 \times R_1 \end{matrix} } \begin{bmatrix} 1&1&|&1&0\\0&2&|&-2&1 \end{bmatrix} \] paso 2 \[ \color{red}{\begin{matrix} \\ (1/2)R_2 \end{matrix} } \begin{bmatrix} 1&1&|&1&0\\0&1&|&-1&1/2 \end{bmatrix} \] paso 3 \[ \color{red}{\begin{matrix} R_1 - R_2 \\ \\ \end{matrix} } \begin{bmatrix} 1&0&|&2&-1/2\\0&1&|&-1&1/2 \end{bmatrix} \] El inverso de A es el 2 × 2 matriz en el lado derecho dada por \[ A^{-1} = \begin{bmatrix} 2&-1/2\\-1&1/2 \end{bmatrix} \]

Ejemplo 3
Encuentre la inversa de la matriz A dada por
\[ A = \begin{bmatrix}-2&2&0 \\ 2&1&3\\ -2&4&-2\end{bmatrix} \] si existiera.
Solución
Escribe la matriz aumentada \( [ A | I )\) \[ \begin{bmatrix} -2&2&0&|&1&0&0\\ 2&1&3&|&0&1&0 \\ -2 & 4 & -2 &|& 0 & 0 & 1 \end{bmatrix} \] paso 1 \[ \color{red}{ \begin{matrix} \\ R_2 + R_1 \\ R_3 - R_1 \end{matrix} } \begin{bmatrix} -2&2&0&|&1&0&0\\ 0&3&3&|&1&1&0 \\ 0 & 2 & -2 &|& -1 & 0 & 1 \end{bmatrix} \] paso 2 \[ \color{red}{ \begin{matrix} \\ \\ R_3 - (2/3) R_2 \\ \end{matrix} } \begin{bmatrix} -2&2&0&|&1&0&0\\ 0&3&3&|&1&1&0 \\ 0 & 0 & - 4&|& -5/3 & -2/3 & 1 \end{bmatrix} \] paso 3 \[ \color{red}{ \begin{matrix} \\ \\ (-1/4)R_3 \\ \end{matrix}} \begin{bmatrix} -2&2&0&|&1&0&0\\ 0&3&3&|&1&1&0 \\ 0 & 0 & 1&|& 5/12 & 1/6 & -1/4 \end{bmatrix} \] paso 4 \[ \color{red}{ \begin{matrix} \\ R_2 - 3\times R_3 \\ \\ \end{matrix} } \begin{bmatrix} -2&2&0&|&1&0&0\\ 0&3&0&|&-1/4&1/2&3/4 \\ 0 & 0 & 1&|& 5/12 & 1/6 & -1/4 \end{bmatrix} \] paso 5 \[ \color{red}{ \begin{matrix} \\ (1/3) R_2 \\ \\ \end{matrix}} \begin{bmatrix} -2&2&0&|&1&0&0\\ 0&1&0&|&-1/12&1/6&1/4 \\ 0 & 0 & 1&|& 5/12 & 1/6 & -1/4 \end{bmatrix} \] paso 6 \[ \color{red}{ \begin{matrix} R_1- 2\times R_2 \\ \\ \\ \end{matrix} } \begin{bmatrix} -2&0&0&|&7/6&-1/3&-1/2\\ 0&1&0&|&-1/12&1/6&1/4 \\ 0 & 0 & 1&|& 5/12 & 1/6 & -1/4 \end{bmatrix} \] paso 7 \[ \color{red}{ \begin{matrix} (-1/2) R_1 \\ \\ \\ \end{matrix} } \begin{bmatrix} 1&0&0&|&-7/12&1/6&1/4\\ 0&1&0&|&-1/12&1/6&1/4 \\ 0 & 0 & 1&|& 5/12 & 1/6 & -1/4 \end{bmatrix} \] por eso \[ A^{-1} = \begin{bmatrix} -7/12&1/6&1/4\\ -1/12&1/6&1/4 \\ 5/12 & 1/6 & -1/4 \end{bmatrix} \]
Más ejemplos sobre cómo encontrar matriz inversa usando operaciones de fila están incluidos.

Encuentre el Inverso de una Matriz Cuadrada Usando Menores, Cofactores y Adjugado

Este método se explica mediante un ejemplo numérico. La matriz A se da a continuación.
\[ A = \begin{bmatrix} -1&0&1\\ 2&-1&2 \\ -1 & 2 & 1 \end{bmatrix} \] a) Encuentre las matrices de menores y cofactores, la adjunta y la inversa de A.
Matriz de Menores
La entrada \( M_{i,j} \) de la matriz de menores de la matriz A viene dada por el determinante obtenido al eliminar la fila \( i^{th}\) y la \( j^{th}\) columna.

Para encontrar \( M_{1,1} \), elimine la fila 1 y la columna 1 de la matriz A y encuentre el determinante de la matriz restante de 2 por 2 de la siguiente manera: \( M_{1,1} = Det \begin{bmatrix} .&.&.\\ .&-1&2 \\ .& 2 & 1 \end{bmatrix} = -1 - 4 = -5\)

Para encontrar \( M_{1,2} \), elimine la fila 1 y la columna 2 de la matriz A y encuentre el determinante de la matriz restante de 2 por 2 de la siguiente manera: \( M_{1,2} = Det \begin{bmatrix} .&.&.\\ 2&.&2 \\ -1 & . & 1 \end{bmatrix} = 2 -(-2) = 4 \)

Para encontrar \( M_{1,3} \), elimine la fila 1 y la columna 3 de la matriz A y encuentre el determinante de la matriz restante de 2 por 2 de la siguiente manera: \( M_{1,3} = Det \begin{bmatrix} .&.&.\\ 2&-1&. \\ -1 & 2 & . \end{bmatrix} = 4 - 1 = 3 \)

Para encontrar \( M_{2,1} \), elimine la fila 2 y la columna 1 de la matriz A y encuentre el determinante de la matriz restante de 2 por 2 de la siguiente manera: \( M_{2,1} = Det \begin{bmatrix} .&0&1\\ .&.&. \\ . & 2 & 1 \end{bmatrix} = 0 - 2 = - 2 \)
...
...
Las entradas restantes están dadas por: \( M_{2,2} = 0 \) , \( M_{2,3} = -2 \) , \( M_{3,1} = 1\) , \( M_{3,2} = -4\) , \( M_{3,3} = 1\).
La matriz de menores M viene dada por
\( M = \begin{bmatrix} -5&4&3\\ -2&0&-2\\ 1&-4&1 \end{bmatrix} \)
Matriz de Cofactores
Las entradas \( C_{i,j} \) de la matriz de cofactores C de la matriz A están dadas por \( C_{i,j} = (-1)^{i+j}M{i,j} \)

Una evaluación de las entradas \( C_{i,j} \) da:
\( C_{1,1} = (-1)^{1+1} M_{1,1} = -5 \)
\( C_{1,2} = (-1)^{1+2} M_{1,2} = - 4 \)
\( C_{1,3} = (-1)^{1+3} M_{1,3} = 3 \)
\( C_{2,1} = (-1)^{2+1} M_{2,1} = 2 \)
\( C_{2,2} = (-1)^{2+2} M_{2,2} = 0 \)
\( C_{3,1} = (-1)^{3+1} M_{3,1} = 1 \)
\( C_{3,2} = (-1)^{3+2} M_{3,2} = 4 \)
\( C_{3,3} = (-1)^{3+3} M_{3,1} = 1 \)
Por tanto, la matriz C de cofactores está dada por \( C = \begin{bmatrix} -5&-4&3\\ 2&0&2\\ 1&4&1 \end{bmatrix} \)
Adjugado (o adjunto) de una matriz
El adjunto (o adjunto) de la matriz A es la transpuesta de su matriz de cofactores C.
\( Adyuvante (A) = C^T = \begin{bmatrix} -5&2&1\\ -4&0&4\\ 3&2&1 \end{bmatrix} \)
Matriz inversa
Ahora necesitamos encontrar el determinante D de la matriz A.
Usando la primera fila de la matriz A y los menores correspondientes ya encontrados, D viene dado por
\( D = det\begin{bmatrix} -1&0&1\\ 2&-1&2 \\ -1 & 2 & 1 \end{bmatrix} = A_{11}M_{1,1} - A_{1,2}M_{1,2} + A_{1,3}M_{1,3} = 8\)
La inversa de \( A \) viene dada por
\( A^{-1} = \dfrac{1}{D} C^T = \dfrac{1}{8} \begin{bmatrix} -5&2&1\\ -4&0&4\\ 3&2&1 \end{bmatrix} = \begin{bmatrix} -\dfrac{5}{8}&\dfrac{1}{4}&\dfrac{1}{8}\\ -\dfrac{1}{2}&0&\dfrac{1}{2}\\ \dfrac{3}{8}&\dfrac{1}{4}&\dfrac{1}{8}\end{bmatrix}\)

Fórmula para la inversa de una matriz de 2 por 2

Usando cualquiera de los dos métodos descritos anteriormente, se puede demostrar que la inversa de la matriz A dada por \[ A = \begin{bmatrix} a & b\\ c & d \\ \end{bmatrix} \] is given by \[ A^{-1} = \dfrac{1}{ad - bc}\begin{bmatrix} d & -b\\ -c & a \\ \end{bmatrix} \]

Propiedades de Matrices Inversas

Una matriz que tiene una inversa se llama matriz invertible.

1. Si A es una matriz invertible, su inversa es única.
   
2. \( A A^{-1} = A^{-1} A = I \)
   
3. Si las matrices A y B son invertibles, entonces:\( (AB)^{-1} = B^{-1}A^{-1} \)
   
4. Una matriz es invertible si y solo si su determinante no es igual a cero.
   
5. Una matriz cuyo determinante no es igual a cero se llama no singular.
   
6. \( (A^T)^{-1} = (A^{-1})^T \)
   
7. \( Det(A^{-1}) = \dfrac{1}{Det(A)} \)
   
8. \( (A^{-1})^{-1} = A \)

Preguntas sobre Matrices Inversas

• Pregunta 1
  Use el método de reducción por filas para encontrar el inverso de las siguientes matrices:
  \( A = \begin{bmatrix} -1&-1&1\\ 2&0&-2 \\ 1 & 1 & 1 \end{bmatrix} \) , \( B = \begin{bmatrix} 1&0&1&2\\ -1& 1 & 2 & 0 \\ -2& 0 & 1 & 2 \\ 0 & 0 & 0 & 1 \end{bmatrix} \)
  
• Pregunta 2
  Usa el método de los cofactores para encontrar la inversa de la siguiente matriz.
  \( A = \begin{bmatrix} -1&0&3\\ 3&2&2 \\ 0& 0 & 1 \end{bmatrix} \)
  
• Pregunta 3
  A, B y C son matrices de 2 por 2. Las matrices B y C están dadas por:
  \[ B = \begin{bmatrix} -1&-1\\ -2& 1 \end{bmatrix} , C = \begin{bmatrix} 2 & -1\\ -2 & 2 \end{bmatrix} \] Encuentre la matriz A tal que AB = C.
  
• Pregunta 4
  ¿Para qué valor(es) de k es invertible cada una de las matrices dadas a continuación?
  a) \( \begin{bmatrix} k & -1 & 4\\ 2 & 0 & 1\\ -1 & 0 & -1 \end{bmatrix} \) , b) \( \begin{bmatrix} k & -1 \\ -1 & 3 \end{bmatrix} \) , c) \( \begin{bmatrix} k & -1 & 4\\ 0 & k + 1 & 1\\ 0 & 0 & k -3 \end{bmatrix} \)
  
• Pregunta 5
  Las matrices cuadradas P, Q, R y S son de la misma dimensión e invertibles tales que \[ P = Q R^{-1} S \] Expresar (o determinar) \( R\) en términos de \( P \), \( Q\) y \( S \) o/y sus inversas.
  
  
• Pregunta 6
  La matriz A está dada por
  \( A = \begin{bmatrix} a & 0 & 0 & 0\\ 0 & b & 0 & 0 \\ 0 & 0 & c & 0\\ 0 & 0 & 0 & d \end{bmatrix} \)
  Encuentre una fórmula para la inversa de la matriz A si ninguno de los parámetros a, b, c y d es igual a cero.
  
• Pregunta 7
  Usa la matriz inversa para resolver el sistema de ecuaciones \( \begin{bmatrix} 1&0&1&2\\ -1& 1 & 2 & 0 \\ -2& 0 & 1 & 2 \\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x_1\\ x_2 \\ x_3\\ x_4 \end{bmatrix} = \begin{bmatrix} 0\\ 1 \\ -1\\ 2 \end{bmatrix} \)
  
• Pregunta 8
  ¿Cuál es el método más eficiente para resolver los siguientes sistemas de ecuaciones?
  \( A X_1 = B_1 \) , \( A X_2 = B_2 \) , \( A X_3 = B_3 \) ... \( A X_i = B_i \)
  
• Pregunta 9
  A y B son matrices invertibles de la misma dimensión relacionadas por: \( A^{-1} = A B \).
  Encuentre B en términos de A o su inversa.
  
• Pregunta 10
  1) Dé un ejemplo de matrices A y B de 2 por 2 tales que ni A ni B sean invertibles pero A + B sí lo sea.
  2) Dé un ejemplo de matrices A y B de 2 por 2 tales que ni A ni B sean invertibles, pero A - B es invertible.
  
• Pregunta 11
  Use cualquiera de los dos métodos para encontrar una fórmula para el inverso de una matriz de 2 por 2 (ya se da arriba sin prueba).
  
• Pregunta 12
  El sistema de ecuaciones en forma matricial
  \( A X = B \)
  tiene las siguientes soluciones: \( X_1 = \begin{bmatrix} -1\\ 2 \\ 3 \end{bmatrix} \) for \( B_1 = \begin{bmatrix} 2\\ 13 \\ 3 \end{bmatrix} \) , \( X_2 = \begin{bmatrix} 0\\ -1 \\ 1 \end{bmatrix} \) for \( B_2 = \begin{bmatrix} 4\\ 2 \\ 2 \end{bmatrix} \) , \( X_3 = \begin{bmatrix} 1\\ 1 \\ 1 \end{bmatrix} \) for \( B_3 = \begin{bmatrix} 4\\ 5 \\ 3 \end{bmatrix} \).
  Encuentra X para \( B = \begin{bmatrix} 1\\ -9 \\ -1 \end{bmatrix} \).

Soluciones a las preguntas anteriores

• Solución a la pregunta 1
  Inversa de la matriz A
  Escribe la matriz aumentada \( [ A | I ] \) \[ \begin{bmatrix} -1&-1&1&|&1&0&0\\ 2&0&-2&|&0&1&0 \\ 1 & 1 & 1 &|& 0 & 0 & 1 \end{bmatrix} \]
  paso 1 \[ \color{red}{ \begin{matrix} -R_1\\ \\ \\ \end{matrix} } \begin{bmatrix} 1&1&-1&|&-1&0&0\\ 2&0&-2&|&0&1&0 \\ 1 & 1 & 1 &|& 0 & 0 & 1 \end{bmatrix} \]
  paso 2 \[ \color{red}{ \begin{matrix} \\ R_2-2R_1 \\ \\ \end{matrix} } \begin{bmatrix} 1&1&-1&|&-1&0&0\\ 0&-2&0&|&2&1&0 \\ 1 & 1 & 1 &|& 0 & 0 & 1 \end{bmatrix} \]
  paso 3 \[ \color{red}{ \begin{matrix} \\ \\ R_3-R_1\\ \end{matrix} } \begin{bmatrix} 1&1&-1&|&-1&0&0\\ 0&-2&0&|&2&1&0 \\ 0 & 0 & 2 &|& 1 & 0 & 1 \end{bmatrix} \]
  paso 4 \[ \color{red}{ \begin{matrix} \\ R_2=(-1/2)R_2\\ R_3=(1/2)R_3\\ \end{matrix} } \begin{bmatrix} 1&1&-1&|&-1&0&0\\ 0&1&0&|&-1&-1/2&0 \\ 0 & 0 & 1 &|& 1/2 & 0 & 1/2 \end{bmatrix} \]
  paso 5 \[ \color{red}{ \begin{matrix} R_1+R_3\\ \\ \\ \end{matrix} } \begin{bmatrix} 1&1&0&|&-1/2&0&1/2\\ 0&1&0&|&-1&-1/2&0 \\ 0 & 0 & 1 &|& 1/2 & 0 & 1/2 \end{bmatrix} \]
  paso 6 \[ \color{red}{ \begin{matrix} R_1-R_2\\ \\ \\ \end{matrix} } \begin{bmatrix} 1&0&0&|&1/2&1/2&1/2\\ 0&1&0&|&-1&-1/2&0 \\ 0 & 0 & 1 &|& 1/2 & 0 & 1/2 \end{bmatrix} \]
  La inversa de la matriz A es la matriz de 3 por 3 del lado derecho. Por eso
  \[ A^{-1} = \begin{bmatrix} 1/2&1/2&1/2\\ -1&-1/2&0 \\ 1/2 & 0 & 1/2 \end{bmatrix} \]
  
  Inversa de la matriz B
  Escribe la matriz aumentada \( [ B | I ]\) \[ \begin{bmatrix} 1&0&1&2 & |&1&0&0&0\\ -1& 1 & 2 & 0 &|&0&1&0&0 \\ -2& 0 & 1 & 2 &|& 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 & |& 0 & 0 & 0 & 1 \end{bmatrix} \]
  paso 1 \[ \color{red}{ \begin{matrix} \\ R_2+R_1\\ R_3+2R_1\\ \\ \end{matrix} } \begin{bmatrix} 1&0&1&2 & |&1&0&0&0\\ 0& 1 & 3 & 2 &|&1&1&0&0 \\ 0& 0 & 3 & 6 &|& 2 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 & |& 0 & 0 & 0 & 1 \end{bmatrix} \]
  
  paso 2 \[ \color{red}{ \begin{matrix} \\ \\ (1/3) R_3\\ \\ \end{matrix} } \begin{bmatrix} 1&0&1&2 & |&1&0&0&0\\ 0& 1 & 3 & 2 &|&1&1&0&0 \\ 0& 0 & 1 & 2 &|& 2/3 & 0 & 1/3 & 0\\ 0 & 0 & 0 & 1 & |& 0 & 0 & 0 & 1 \end{bmatrix} \]
  paso 3 \[ \color{red}{ \begin{matrix} R_1-2R_4\\ R_2-2R_4\\ R_3-2R_4\\ \\ \end{matrix} } \begin{bmatrix} 1&0&1&0 & |&1&0&0&-2\\ 0& 1 & 3 & 0 &|&1&1&0&-2 \\ 0& 0 & 1 & 0 &|& 2/3 & 0 & 1/3 & -2\\ 0 & 0 & 0 & 1 & |& 0 & 0 & 0 & 1 \end{bmatrix} \]
  paso 4 \[ \color{red}{ \begin{matrix} R_1-R_3\\ R_2-3R_3\\ \\ \\ \end{matrix} } \begin{bmatrix} 1&0&1&0 & |&1/3&0&-1/3&0\\ 0& 1 & 0 & 0 &|&-1&1&-1&4 \\ 0& 0 & 1 & 0 &|& 2/3 & 0 & 1/3 & -2\\ 0 & 0 & 0 & 1 & |& 0 & 0 & 0 & 1 \end{bmatrix} \]
  La inversa de la matriz B es la matriz de 4 por 4 del lado derecho. Por eso
  \[ B^{-1} = \begin{bmatrix} 1/3&0&-1/3&0\\ -1&1&-1&4 \\ 2/3 & 0 & 1/3 & -2\\ 0 & 0 & 0 & 1 \end{bmatrix} \]
  
• Solución a la pregunta 2
  Primero encontramos a los menores.
  \( M_{1,1} = Det \begin{bmatrix} .&.&.\\ .&2&2 \\ .& 0 & 1 \end{bmatrix} = 2\) , \( M_{1,2} = Det \begin{bmatrix} .&.&.\\ 3&.&2 \\ 0& . & 1 \end{bmatrix} = 3\) , \( M_{1,3} = Det \begin{bmatrix} .&.&.\\ 3&2&. \\ 0& 0 & . \end{bmatrix} = 0 \)
  
  \( M_{2,1} = Det \begin{bmatrix} .&0&3\\ .&.&. \\ .& 0 & 1 \end{bmatrix} = 0\) , \( M_{2,2} = Det \begin{bmatrix} -1&.&3\\ . & . & . \\ 0& . & 1 \end{bmatrix} = -1\) , \( M_{2,3} = Det \begin{bmatrix} -1&0&.\\ . & . & .\\ 0& 0 & . \end{bmatrix} = 0\)
  
  \( M_{3,1} = Det \begin{bmatrix} .&0&3\\ .&2&2 \\ . & . & . \end{bmatrix} = - 6\) , \( M_{3,2} = Det \begin{bmatrix} -1&.&3\\ 3&.&2 \\ . & . & . \end{bmatrix} = - 11\) , \( M_{3,3} = Det \begin{bmatrix} -1&0& .\\ 3&2& . \\ . & . & . \end{bmatrix} = - 2\)
  Matriz C de cofactores cuyas entradas definidas se definen como
  \( C_{i,j} = (-1)^{i+j} M_{i,j} \) \[ C = \begin{bmatrix} 2&-3&0\\ 0&-1&0 \\ - 6 & 11 & -2 \end{bmatrix} \]
  Necesitamos encontrar D el determinante de A usando la tercera fila (¡tiene 2 ceros!)
  \( D = A_{3,3} M_{3,3} = - 2 \)
  La inversa de A está dada por \( A^{-1} = \dfrac{1}{D} C^T = -\dfrac{1}{2} \begin{bmatrix} 2&0&-6\\ -3&-1&11\\ 0&0&-2 \end{bmatrix} = \begin{bmatrix} -1&0&3\\ \dfrac{3}{2}& \dfrac{1}{2} & -\dfrac{11}{2}\\ 0&0&1\end{bmatrix}\)
  
• Solución a la pregunta 3
  Dada
  \( A B = C \)
  A la derecha multiplica ambos lados por \( B^{-1} \)
  \( A B B^{-1} = C B^{-1}\)
  Usa la asociatividad en el lado izquierdo
  \( A (B B^{-1}) = C B^{-1} \)
  Simplificar
  \( A I = C B^{-1} \)
  \( A = C B^{-1} \)
  Use la fórmula para el inverso de una matriz de 2 por 2 para encontrar el inverso de B.
  \( Det(B) = -3 \)
  \( B^{-1} = - \dfrac{1}{3} \begin{bmatrix} 1&1\\ 2& -1 \end{bmatrix} \)
  
  \( A = C B^{-1} = \begin{bmatrix} 2 & -1\\ -2 & 2 \end{bmatrix} (- \dfrac{1}{3}) \begin{bmatrix} 1&1\\ 2& -1 \end{bmatrix} = \begin{bmatrix} 0&-1\\ -2/3& 4/3 \end{bmatrix}\)
  
  Nota: puede comprobar la respuesta de la matriz A sustituyendo en la ecuación \( A B = C \)
  
• Solución a la pregunta 4
  Una matriz es invertible si su determinante no es igual a cero.
  a) Utilizando la segunda columna,
  Det\( \begin{bmatrix} k & -1 & 4\\ 2 & 0 & 1\\ -1 & 0 & -1 \end{bmatrix} = - 1\) La matriz es invertible para cualquier k real
  
  b) Det\( \begin{bmatrix} k & -1 \\ -1 & 3 \end{bmatrix} = 3k - 1\)
  \( 3k - 1 \ne 0 \)
  \( k \ne 1/3 \)
  La matriz del apartado b) es invertible para todos los valores reales de k distintos de 1/3.
  
  c) La matriz dada es una matriz triangular superior y su determinante es igual al producto de los términos en la diagonal de izquierda a derecha.
  Det \( \begin{bmatrix} k & -1 & 4\\ 0 & k + 1 & 1\\ 0 & 0 & k -3 \end{bmatrix} k(k+1)(k-3)\)
  \( k(k+1)(k-3) \ne 0 \)
  La matriz dada es invertible si k no es igual a 0, - 1 o 3.
  
• Solución a la pregunta 5
  Multiplica a la derecha los dos lados de la ecuación por \( S^{-1} \)
  \( P S^{-1} = Q R^{-1} S S^{-1} \)
  simplificar
  \( P S^{-1} = Q R^{-1} I \)
  \( P S^{-1} = Q R^{-1} \)
  Multiplica a la izquierda los dos lados de la ecuación por \( Q^{-1} \)
  \( Q^{-1} P S^{-1} = Q^{-1} Q R^{-1} \)
  simplificar
  \( Q^{-1} P S^{-1} = I R^{-1}\)
  \( Q^{-1} P S^{-1} = R^{-1} \)
  Toma el inverso de ambos lados
  \( (Q^{-1} P S^{-1})^{-1} = (R^{-1})^{-1} \)
  simplificar
  \( R = S P^{-1} Q \)
  
• Solución a la pregunta 6
  Escribe la matriz aumentada \( [ A | I ]\)
  
  \( \begin{bmatrix} a & 0 & 0 & 0&|&1&0&0&0\\ 0 & b & 0 & 0&|&0&1&0&0 \\ 0 & 0 & c & 0 &|& 0 & 0 & 1 & 0\\ 0 & 0 & 0 & d &|& 0 & 0 & 0 & 1 \end{bmatrix} \)
  
  Multiplique la fila (1) por 1/a, la fila (2) por 1/b, la fila (3) por 1/c y la fila (4) por 1/d y simplifique
  
  \( \begin{bmatrix} 1 & 0 & 0 & 0&|&1/a&0&0&0\\ 0 & 1 & 0 & 0&|&0&1/b&0&0 \\ 0 & 0 & 1 & 0 &|& 0 & 0 & 1/c & 0\\ 0 & 0 & 0 & 1 &|& 0 & 0 & 0 & 1/d \end{bmatrix} \)
  
  La inversa de la matriz dada es
  
  \( A^{-1} = \begin{bmatrix} 1/a&0&0&0\\ 0&1/b&0&0 \\ 0 & 0 & 1/c & 0\\ 0 & 0 & 0 & 1/d \end{bmatrix} \)
  
• Solución a la pregunta 7
  El sistema es de la forma
  A X = B with A = \( \begin{bmatrix} 1&0&1&2\\ -1& 1 & 2 & 0 \\ -2& 0 & 1 & 2 \\ 0 & 0 & 0 & 1 \end{bmatrix} \) , \( B =\begin{bmatrix} 0\\ 1 \\ -1\\ 2 \end{bmatrix} \) and \( X = \begin{bmatrix} x_1\\ x_2 \\ x_3\\ x_4 \end{bmatrix} \)
  Multiplique a la derecha ambos lados de la ecuación por \( A^{-1} \) y simplifique.
  \( A^{-1} A X = A^{-1} B \)
  \( I_3 X = A^{-1} B , I_3 \) es la matriz identidad de 3 por 3
  Simplifica lo anterior
  \( X = A^{-1} B \)
  La inversa de la matriz A se calculó en la pregunta 1 y viene dada por (es la matriz B en la pregunta 1)
  \( A^{-1} = \begin{bmatrix} 1/3&0&-1/3&0\\ -1&1&-1&4 \\ 2/3 & 0 & 1/3 & -2\\ 0 & 0 & 0 & 1 \end{bmatrix} \)
  \( \begin{bmatrix} x_1\\ x_2 \\ x_3\\ x_4 \end{bmatrix} = A^{-1} B = \begin{bmatrix} 1/3&0&-1/3&0\\ -1&1&-1&4 \\ 2/3 & 0 & 1/3 & -2\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 0\\ 1 \\ -1\\ 2 \end{bmatrix} = \begin{bmatrix}\dfrac{1}{3}\\ 10\\ -\dfrac{13}{3}\\ 2\end{bmatrix}\)
  
• Solución a la pregunta 8
  Dado que la matriz A es común a todos los sistemas dados, el método más eficiente para resolver sistemas de ecuaciones de la forma
  \( A X_1 = B_1 \) , \( A X_2 = B_2 \) , \( A X_3 = B_3 \) ... \( A X_2 = B_i \)
  es encontrar la inversa de la matriz A y resolver de la siguiente manera (ver pregunta 7 arriba)
  \( X_1 = A^{-1} B_1 \) , \( X_2 = A^{-1} B_2 \) , \( X_3 = A^{-1} B_3 \) ... \( X_i = A^{-1} B_i \)
  
• Solución a la pregunta 9
  A y B son matrices invertibles de la misma dimensión relacionadas por: \( A^{-1} = A B \).
  Encuentre B en términos de A o su inversa.
  Multiplique la ecuación por la derecha por \( A^{-1} \)
  \( A^{-1} A^{-1} = A^{-1} A B \)
  simplificar
  \( A^{-1} A^{-1} = I B \)
  simplificar a
  \( B = A^{-2}\)
  
• Solución a la pregunta 10
  Hay muchas respuestas posibles a ambas partes de esta pregunta.
  1) \(A = \begin{bmatrix} 1 & 1\\ 0 & 0 \\ \end{bmatrix} , B = \begin{bmatrix} 0 & 0\\ - 1 & 1 \\ \end{bmatrix} \) , \(A + B = \begin{bmatrix} 1 & 1\\ - 1 & 0 \\ \end{bmatrix} \)
  
  2) \(A = \begin{bmatrix} 3 & 1\\ 0 & 0 \\ \end{bmatrix} , B = \begin{bmatrix} 0 & 0\\ - 1 & 4 \\ \end{bmatrix} \) , \(A - B = \begin{bmatrix} 3 & 1\\ 1 & - 4 \\ \end{bmatrix} \)
  Comprobar que el determinante de las matrices A y B es igual a cero y por tanto no invertible. Comprueba que los determinantes de A + B y A - B no son iguales a cero y por lo tanto invertibles.
  
• Solución a la pregunta 11
  Dejar \(A = \begin{bmatrix} a & b\\ c & d \\ \end{bmatrix} \)
  Utilizaremos el método de los cofactores. Primero calculamos los menores
  \( M_{1,1} = d\) , \( M_{1,2} = c\) , \( M_{2,1} = b\) , \( M_{2,2} = a\)
  Luego los cofactores usando la fórmula: \( C_{i,j} = (-1)^{i+j}M_{i,j} \)
  \( C_{1,1} = d\) , \( C_{1,2} = - c\) , \( C_{2,1} = - b\) , \( C_{2,2} = a\)
  La determinante de A es
  \( D = a d - b c \)
  \( A^{-1} = \dfrac{1}{a d - b c} \begin{bmatrix} d & - c\\ - d & a \\ \end{bmatrix}^T = \dfrac{1}{a d - b c} \begin{bmatrix} d & - d\\ - c & a \\ \end{bmatrix} \)
  
• Solución a la pregunta 12
  Las soluciones se pueden escribir en forma matricial de la siguiente manera
  \( A \begin{bmatrix} -1 & 0 & 1 \\ 2 & - 1 & 1\\ 3 & 1 & 1 \end{bmatrix} = \begin{bmatrix} 5 & 4 & 4\\ 17 & 2 & 5\\ 5 & 2 & 3 \end{bmatrix} \)
  lo que da
  \( A = \begin{bmatrix} 5 & 4 & 4\\ 17 & 2 & 5\\ 5 & 2 & 3 \end{bmatrix} \begin{bmatrix} -1 & 0 & 1 \\ 2 & - 1 & 1\\ 3 & 1 & 1 \end{bmatrix}^{-1} \)
  lo que da
  \( A^{-1} = \begin{bmatrix} -1 & 0 & 1 \\ 2 & - 1 & 1\\ 3 & 1 & 1 \end{bmatrix} \begin{bmatrix} 5 & 4 & 4\\ 17 & 2 & 5\\ 5 & 2 & 3 \end{bmatrix}^{-1} \)
  La solución X está dada por
  \( X = A^{-1} B = \begin{bmatrix} -1 & 0 & 1 \\ 2 & - 1 & 1\\ 3 & 1 & 1 \end{bmatrix} \begin{bmatrix} 5 & 4 & 4\\ 17 & 2 & 5\\ 5 & 2 & 3 \end{bmatrix}^{-1} \begin{bmatrix} 1\\ -9 \\ -1 \end{bmatrix} = \begin{bmatrix} 1\\ -2 \\ -1 \end{bmatrix} \)

Más Referencias y Enlaces a Matrices

• Matrices con Ejemplos y Preguntas con Soluciones.
  
• Encuentre la inversa de una matriz usando la reducción de filas
  
• multiplicación de matrices usando una aplicación.
• Encuentra matriz inversa - Calculadora.
  
• Encuentra el inverso de la matriz de 3 por 3 - Calculadora.
  
• Solucionador paso a paso para encontrar la inversa de una matriz de 3 por 3.
  
• Solucionador paso a paso para calcular el determinante de una matriz de 3 por 3.