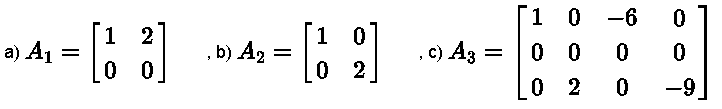Presentamos las definiciones de espacios de columnas y filas de una matriz utilizando ejemplos con soluciones detalladas.
Sea \( A \) una matriz de \( m \times n \).
El espacio columna de la matriz \( A \), denotado por Col A, es el conjunto de todas las combinaciones lineales de las columnas de la matriz A.
Si
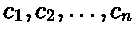son las columnas de la matriz \( A \), entonces
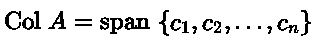Nota que las columnas 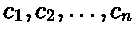pueden no ser independientes y en lo que sigue veremos ejemplos de cómo encontrar la base de Col A seleccionando solo las columnas independientes.
El rango de la matriz \( A \) es la dimensión de Col A, que viene dada por el número de vectores en la base de Col A.
Ejemplo 1
Encuentre la base del espacio columna y el rango de cada una de las matrices:
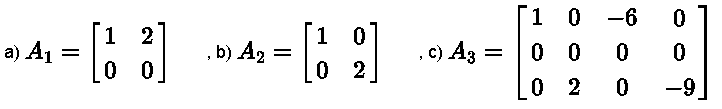
Solución al Ejemplo 1
a)
Sean \( c_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \) y \( c_2 = \begin{bmatrix} 2 \\ 0 \end{bmatrix} \) las columnas de la matriz \( A_1 \).
Note que \( c_2 = 2 c_1 \) y por lo tanto \( c_1 \) y \( c_2 \) NO son independientes. Como resultado, solo necesitamos una columna para generar \( \text{Col}\; A_1 \).
Por lo tanto, la base \( B \) de \( \text{Col} \; A_1 \) está dada por: \( B = \{c_1\} \) o \( B = \left\{ \begin{bmatrix} 1 \\ 0 \end{bmatrix} \right\} \)
\[ \text{Col} \; A_1 = \text{span} \{c_1\} \]
La base de \( \text{Col} \; A_1 \) tiene un vector y por lo tanto \( \text{Rango} (A_1) = 1 \).
b)
Sean \( c_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \) y \( c_2 = \begin{bmatrix} 0 \\ 2 \end{bmatrix} \) las columnas de la matriz \( A_2 \). Note que \( c_1 \) y \( c_2 \) son independientes. Como resultado, necesitamos ambas columnas \( c_1 \) y \( c_2 \) para generar \( \text{Col}\; A_2 \).
La base \( B \) de \( \text{Col} \; A_2 \) está dada por: \( B = \{c_1,c_2\} \) o \( B = \left\{\begin{bmatrix} 1 \\ 0 \end{bmatrix} , \begin{bmatrix} 0 \\ 2 \end{bmatrix} \right\} \)
\[ \text{Col} \; A_2 = \text{span} \{c_1,c_2\} \]
La base de \( \text{Col} \; A_2 \) tiene dos vectores y por lo tanto \( \text{Rango} (A_2) = 2 \).
c)
Sean \( c_1 = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \), \( c_2 = \begin{bmatrix} 0 \\ 0 \\ 2 \end{bmatrix} \), \( c_3 = \begin{bmatrix} -6 \\ 0 \\ 0 \end{bmatrix} \) y \( c_4 = \begin{bmatrix} 0 \\ 0 \\ -9 \end{bmatrix} \) las columnas de la matriz \( A_3 \).
Note que \( c_1 \) y \( c_2 \) son independientes. Sin embargo, \( c_3 \) y \( c_4 \) dependen de \(c_1\) y \( c_2\) de la siguiente manera: \( c_3 = - 6 c_1 \) y \( c_4 = - \dfrac{9}{2} c_2 \).
Por lo tanto, la base \( B \) de \( \text{Col} \; A_3 \) está dada por: \( B = \{c_1,c_2\} \) o \( B = \left\{\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} , \begin{bmatrix} 0 \\ 0 \\ 2 \end{bmatrix} \right\} \)
\[ \text{Col} \; A_3 = \text{span} \{c_1,c_2\} \]
La base de \( \text{Col} \; A_3 \) tiene dos vectores y por lo tanto \( \text{Rango} (A_3) = 2 \).
Ejemplo 2
Encuentre la base del espacio columna y el rango de la matriz \[ A = \begin{bmatrix} 1 & -2 & 0 & 4\\ -1 & 3 & 1 & 0\\ 0 & -1 & -1 & -4 \end{bmatrix} \]
Solución al Ejemplo 2
Como se vio en el ejemplo 1, la base de \( Col \; A \) está dada por las columnas linealmente independientes de la matriz \( A \). Una forma de determinar qué columnas son linealmente independientes es reescribir la matriz dada en forma escalonada por filas (REF).
Reescriba la matriz \( A \) en forma escalonada por filas
\[ \begin{matrix} \\ \color{red}{R_2+R_1}\\ \\ \end{matrix} \begin{bmatrix} 1 & -2 & 0 & 4\\ 0 & 1 & 1 & 4\\ 0 & -1 & -1 & -4 \end{bmatrix} \]
\[ \begin{matrix} \\ \\ \color{red}{R_3+R_2}\\ \end{matrix} \begin{bmatrix} \color{blue}1 & -2 & 0 & 4\\ 0 & \color{blue}1 & 1 & 4\\ 0 & 0 & 0 & 0 \end{bmatrix} \]
La base de \( \text{Col} \; A \) está dada por la columna en la matriz original correspondiente a las columnas con pivote (el 1 principal en una fila) en la forma escalonada obtenida.
La primera y segunda columna en la matriz reducida tienen cada una un pivote, por lo tanto, la primera y segunda columna en la matriz original forman la base \( B \) de \( \text{Col}\ A \), que está dada por
\[ B = \left\{\begin{bmatrix} 1 \\ -1 \\ 0 \end{bmatrix} , \begin{bmatrix} -2 \\ 3\\ -1 \end{bmatrix} \right\} \]
\[ \text{Col}\ A = \text{span} \left\{ \begin{bmatrix} 1 \\ -1 \\ 0 \end{bmatrix} , \begin{bmatrix} -2 \\ 3\\ -1 \end{bmatrix} \right\} \]
La base de \( \text{Col} \; A \) tiene dos vectores y por lo tanto \( \text{Rango} (A) = 2 \).
Sea \( A \) una matriz de \( m \times n\).
El espacio fila de la matriz \( A \), denotado por \( \text{Row} A \), es el conjunto de todas las combinaciones lineales de las filas de la matriz \( A \). Si \( b_1, b_2, ..., b_m \) son las filas de la matriz \( A \), entonces
\[ \text{Row} \; A = \text{span} \; \{b_1, b_2, ..., b_n\} \]
Nota que las filas \( \{b_1, b_2, ..., b_m\} \) pueden no ser independientes y en lo que sigue veremos ejemplos de cómo encontrar la base de \( \text{Row} \; A \) seleccionando solo las filas independientes.
El rango de la matriz \( A \) es la dimensión de \( \text{Row} \; A \), que viene dada por el número de vectores en la base de \( \text{Row} \; A \).
Ejemplo 3
Encuentre la base del espacio fila y el rango de cada una de las matrices: \[ \text{a)} \quad A_1 = \begin{bmatrix} 4 & 8 \\ - 2 & - 4 \end{bmatrix}, \text{b)} \quad A_2 = \begin{bmatrix} 1 & 0 & 5\\ 0 & 2 & 7 \end{bmatrix}, \text{c)} \quad A_3 = \begin{bmatrix} 1 & 0 & -6 & 0\\ 0 & 0 & 0 & 0\\ 0 & 2 & 0 & -9 \end{bmatrix} \]
Solución al Ejemplo 3
a)
Sean \( b_1 = (4,8) \) y \( b_2 = (-2,-4) \) las filas de la matriz \( A_1 \). Note que \( b_2 = - \dfrac{1}{2} b_1 \) y por lo tanto \( b_1 \) y \( b_2 \) NO son independientes. Como resultado, solo necesitamos una fila para generar \( \text{Row}\; A_1 \).
Por lo tanto, la base \( B \) de \( \text{Row} \; A_1 \) está dada por: \( B = \{ b_1\} \) o \( B = \{ (4,8) \} \)
\[ \text{Row} \; A_1 = \text{span} \{ (4,8) \} \]
La base de \( \text{Row} \; A_1 \) tiene un vector y por lo tanto \( \text{Rango} (A_1) = 1 \).
b)
Sean \( b_1 = (1,0,5) \) y \( b_2 = (0,2,7) \) las filas de la matriz \( A_2 \). Note que \( b_1 \) y \( b_2 \) son independientes. Por lo tanto, necesitamos ambas filas para generar \( \text{Row} \; A_2 \).
La base \( B \) de \( \text{Row} \; A_2 \) está dada por: \( B = \{ b_1 , b_2 \} \) o \( B = \{ (1,0,5) , (0,2,7) \} \)
\[ \text{Row} \; A_2 = \text{span} \{ (1,0,5) , (0,2,7) \} \]
La base de \( \text{Row} \; A_2 \) tiene dos vectores y por lo tanto \( \text{Rango} (A_2) = 2 \).
c)
Sean \( b_1 = (1,0,-6,0) \), \( b_2 = (0,0,0,0) \) y \( b_3 = (0,2,0,-9) \) las filas de la matriz \( A_3 \).
Note que \( b_1 \) y \( b_3 \) son independientes; \( b_2 \) es un vector cero que no contribuye en ninguna combinación lineal y por lo tanto no se incluye en la base.
La base \( B \) de \( \text{Row} \; A_3 \) está dada por: \( B = \{ b_1 , b_3 \} \) o \( B = \{ (1,0,-6,0) , (0,2,0,-9) \} \)
\[ \text{Row} \; A_3 = \text{span} \{ (1,0,-6,0) , (0,2,0,-9) \} \]
La base de \( \text{Row} \; A_3 \) tiene dos vectores y por lo tanto \( \text{Rango} (A_3) = 2 \).
Ejemplo 4
Encuentre la base del espacio fila y el rango de la matriz \[ A = \begin{bmatrix} 1 & -2 & 0 & 4\\ 1 & 1 & -1 & - 8 \\ 2 & -1 & -1 & -4 \\ - 3 & 3 & 1 & 0 \end{bmatrix} \]
Solución al Ejemplo 4
Necesitamos encontrar filas independientes entre las filas de la matriz dada. Esto se puede hacer reescribiendo la matriz dada en forma escalonada por filas. Reescriba la matriz \( A \) en forma escalonada por filas \[ \begin{matrix} \\ R_2 - R_1\\ R_3 - 2 R_1\\ R_4 + 3 R_1\\ \end{matrix} \begin{bmatrix} 1 & -2 & 0 & 4\\ 0 & 3 & -1 & -12\\ 0 & 3 & -1 & -12\\ 0 & -3 & 1 & 12 \end{bmatrix} \] \[ \begin{matrix} \\ \frac{1}{3} R_2\\ \\ \\ \end{matrix} \begin{bmatrix} 1 & -2 & 0 & 4\\ 0 & 1 & -1/3 & - 4\\ 0 & 3 & -1 & -12\\ 0 & -3 & 1 & 12 \end{bmatrix} \] \[ \begin{matrix} \\ \\ R_3 - 3 R_2\\ R_4 + 3 R_2\\ \end{matrix} \begin{bmatrix} 1 & -2 & 0 & 4\\ 0 & 1 & -1/3 & - 4\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{bmatrix} \quad (I) \] La base de \( \text{Row} \; A \) está dada por las filas no nulas en la forma escalonada (matriz I) obtenida. Por lo tanto \[ \text{Row}\ A = \text{span} \; \left\{ (1 , -2 , 0 , 4) , (0 , 1 , -1/3 , - 4) \right\} \] La base de \( \text{Row} \; A \) tiene dos vectores y por lo tanto \( \text{Rango} (A) = 2 \).
Si \( A \) es una matriz de \( m \times n \),
Paso 1: Reescribir la matriz \( A \) en forma escalonada por filas como la matriz \( E \)
Paso 2: La base de \( \text{Row} \; A \) es el conjunto de todas las filas no nulas en la matriz \( E \) y \( \text{Row} \; A \) es un subespacio de \( \mathbb{R}^n \)
Paso 3: La base de \( \text{Col} \; A \) es el conjunto de todas las columnas en \( A \) correspondientes a las columnas con pivote en \( E \) y \( \text{Col} A \) es un subespacio de \( \mathbb{R}^m \)
Paso 4: Rango de A = dim\( \text{Row} \; A \) = dim \( \text{Col} \; A \)
Ejemplo 5
Encuentre la base del espacio fila, la base del espacio columna y el rango de la matriz \[ A = \begin{bmatrix} -1 & 3 & 4 & -2\\ 1 & 2 & -2 & 0\\ 2 & -3 & 1 & 0\\ 0 & 5 & 2 & -2 \end{bmatrix} \]
Solución al Ejemplo 5
Paso 1: Escribir la matriz \( A \) en forma escalonada por filas \( E \)
Nota que dado que escribir matrices en forma escalonada no es el tema principal tratado aquí, hemos utilizado una calculadora de reducción por filas para obtener la forma escalonada \( E \) de la matriz dada.
\[ E = \begin{bmatrix} 1 & -3 & -4 & 2\\ 0 & 1 & 2/5 & -2/5\\ 0 & 0 & 1 & -14/39\\ 0 & 0 & 0 & 0 \end{bmatrix} \]
Paso 2: La base \( B \) de \( \text{Row} A \) es el conjunto de todas las filas no nulas en \( E \). Por lo tanto \[ B = \{ (1 , -3 , -4 , 2) , (0 , 1 , 2/5 , -2/5) , (0 , 0 , 1 , -14/39) \} \]
Paso 3: La base \( C \) de \( \text{Col} A \) es el conjunto de todas las columnas en \( A \) correspondientes a las columnas con pivotes en \( E \). Las primeras tres columnas en \( E \) tienen un pivote, por lo tanto, la base es el conjunto de las primeras tres columnas en \( A \). \[ C = \left\{ \begin{bmatrix} -1\\ 1\\ 2\\ 0 \end{bmatrix} , \begin{bmatrix} 3\\ 2\\ -3\\ 5 \end{bmatrix} , \begin{bmatrix} 4\\ -2\\ 1\\ 2 \end{bmatrix} \right\} \]
Paso 4: Las dimensiones de \( \text{Row} \; A \) y \( \text{Col} \; A \) están dadas por
dim \( \text{Row} \; A \) = número de filas en la base \( B \) de \( \text{Row} \; A \) = 3
dim \( \text{Col} \; A \) = número de vectores en la base \( C \) de \( \text{Col} \; A \) = 3
Rango de \( A \) = dim \( \text{Row} \; A \) = dim \( \text{Col} \; A \) = 3
Dada la matriz \( A \) y su forma escalonada por filas \( E \), determine el espacio columna, el espacio fila y el rango de cada matriz.
Soluciones a las Preguntas Anteriores