Números complejos en forma exponencial

Los Los números complejos se escriben en forma exponencial. Las multiplicaciones, divisiones y potencias de números complejos en forma exponencial se explican mediante ejemplos y se refuerzan mediante preguntas con soluciones detalladas.

Forma exponencial de números complejos

Un número complejo en forma estándar \( z = a + ib \) se escribe en forma polar como \[ z = r (\cos(\theta)+ i \sin(\theta)) \] donde \( r = \sqrt{a^2+b^2} \) se denomina módulo de \( z \)
y
\( \tan (\theta) = \left (\dfrac{b}{a} \right) \) , tal que \( 0 \le \theta \lt 2\pi \) , \( \theta\) se llama argumento Ejemplos y preguntas con soluciones. de \(z\)
Las interpretaciones gráficas de \( a \) , \( b \) , \( r \) y \( \theta \) se muestran a continuación para un número complejo en un plano complejo.

plano complejo

Ahora usamos la fórmula de Euler dada por \( \displaystyle e^{i\theta} = \cos \theta + i \sin \theta \) para escribir el número complejo \( z \) en forma exponencial de la siguiente manera: \[ z = r e^{i\theta}\] dónde \( r \) y \( \theta \) como se definió anteriormente.

Ejemplo 1
Traza el número complejo \( z = -1 + i \) en el plano complejo y escríbelo en forma exponencial .
Solución al ejemplo 1
El número complejo \(z = -1 + i = a + i b \) siendo \( a = -1 \) la parte real y \( b = 1 \) la parte imaginaria, se representa como un vector en un plano complejo que se muestra a continuación. Es un vector cuyas componentes son la parte real \( a \) a lo largo del "eje real" y la parte imaginaria \( b \) a lo largo del "eje imaginario". El argumento ángulo \( \theta \) es el ángulo en sentido antihorario con el lado inicial comenzando desde el eje de la parte real positiva. El módulo \( r = \sqrt {a^2+b^2} = \sqrt {(-1)^2+(1)^2} = \sqrt 2\) es la longitud del vector.

gráfica del número complejo z = -1 + i en el plano complejo

\(z = -1 + i = a + i b\)
da \( a = - 1 \) y \( b = 1 \)
\( r = \sqrt {a^2 + b^2} = \sqrt {(-1)^2 + 1^2} = \sqrt {1 + 1} = \sqrt 2\)
Primero necesitamos encontrar el ángulo de referencia \( \theta_r \) que es el ángulo agudo entre el lado terminal de \( \theta \) y el eje de la parte real.
\( \theta_r = \tan^{-1}\left|\dfrac{b}{a}\right| = \tan^{-1}\left|\dfrac{1}{-1}\right| = \tan^{-1} (1) = \dfrac{\pi}{4}\)
La parte real de \(z\) es negativa y su parte imaginaria es positiva, por lo tanto, el lado terminal de \( \theta \) está en el cuadrante II (ver gráfico de \( z \) arriba).
\( \theta \) se calcula de la siguiente manera:
\( \theta = \pi - \theta_r = \pi - \dfrac{\pi}{4} = \dfrac{3\pi}{4}\)
\( z \) en forma exponencial viene dada por
\( z = \sqrt2 e^{i\dfrac{3\pi}{4}} \)

Ejemplo 2
a) Trazar los números complejos: \( i , - 2 , - i , - 1 - 2i \) y \( 1 - i \) en el mismo plano complejo.
b) Trazar en planos complejos separados y escribir los números complejos: \( i , - 2 , - i , - 1 - 2i \) y \( 1 - i \) en forma exponencial .

Solución al ejemplo 2
a) A continuación se muestra la gráfica de todos los números complejos dados en el mismo plano complejo.

Gráfica de números complejos en el ejemplo 2 en un plano complejo

b) Trazar y escribir en formas exponenciales .
1) Sea \( z = i = a + i b \)
da \( a = 0 \) y \( b = 1 \)
\( r = \sqrt {0^2 + 1^2} = 1 \)
\( \tan \theta = \dfrac{1}{0} = indefinido \)
Un ángulo cuya tangente no está definida es un ángulo con lado terminal en el eje imaginario.
De hecho, es más fácil determinar \( \theta = \dfrac{\pi}{2} \) a partir del gráfico de \( z = i \) que se muestra a continuación.
Escribe en forma exponencial : \( \quad z = i = r e^{i\theta} = e^{i\pi/2} \)

gráfico de número complejo i

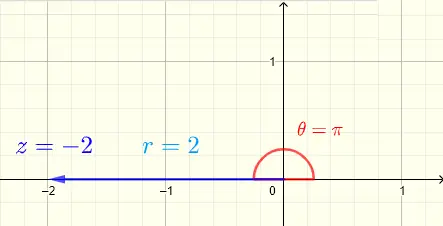
2) Sea \( z = -2 = a + i b \)
da \( a = -2 \) y \( b = 0 \)
\( r = \sqrt {(-2)^2 + 0^2} = 2 \)
\( \tan \theta = \dfrac{0}{-2} = 0 \)
Un ángulo cuya tangente es igual a 0 es un ángulo con lado terminal en el eje real.
Es más fácil determinar \( \theta = \pi \) a partir del gráfico de \( z = -2 \) que se muestra a continuación.
Escribe en forma exponencial : \( \quad z = -2 = r e^{i\theta} = 2 e^{i\pi} \)

trama de número complejo -2

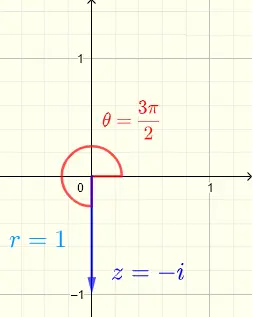
3) Sea \( z = - i = a + i b \)
da \( a = 0 \) y \( b = - 1 \)
\( r = \sqrt {0^2 + (-1)^2} = 1 \)
\( \tan \theta = \dfrac{-1}{0} = indefinido \)
Un ángulo cuya tangente no está definida es un ángulo con lado terminal en el eje imaginario.
Determinamos \( \theta = \dfrac{3\pi}{2} \) a partir de la gráfica de \( z = - i \) que se muestra a continuación.
Escribe en forma exponencial : \( \quad z = - i = r e^{i\theta} = e^{ i 3\pi/2} \)

gráfico de número complejo -i

4) Sea \( z = - 1 -2i = a + i b \)
da \( a = -1 \) y \( b = - 2 \)
\( r = \sqrt {(-1)^2 + (-2)^2} = \sqrt 5 \)
Primero encuentre el ángulo de referencia: \( \tan \theta_r = |\dfrac{-2}{-1}| = 2 \) , \( \theta_r = \arctan 2 \)
\( \theta = \pi + \arctan 2 \approx 4,25\)
Escribe en forma exponencial : \( \quad z = - 1 -2i = r e^{i\theta} = \sqrt 5 e^{i (\pi + \arctan 2 )} \)

gráfico del número complejo -1-2i

5) Sea \( z = 1 - i = a + i b \)
da \( a = 1 \) y \( b = - 1 \)
\( r = \sqrt {(1)^2 + (-1)^2} = \sqrt 2 \)
Primero encuentre el ángulo de referencia: \( \tan \theta_r = |\dfrac{-1}{1}| = 1 \) , \( \theta_r = \dfrac{\pi}{4} \)
\( \theta = 2\pi - \theta_r = 2\pi - \dfrac{\pi}{4} = \dfrac{7\pi}{4} \)
Escribe en forma exponencial : \( \quad z = 1 - i = r e^{i\theta} = \sqrt 2 e^{i ( 7 \pi/4)} \)

gráfico del número complejo 1 - i

Ejemplo 3
Escribe el número complejo \( z = \sqrt2 e^{ i \dfrac{5\pi}{4}} \) en forma estándar.
Solución al ejemplo 3
\( z = \sqrt2 e^{ i \dfrac{5\pi}{4}} \)
Usa la fórmula de Euler
\( = \sqrt2(\cos(\dfrac{5\pi}{4})+ i \sin(\dfrac{5\pi}{4})) \)
Simplificar
\( = \sqrt2(-\dfrac{\sqrt2}{2} - i \dfrac{\sqrt2}{2}) \)
\( = - 1 - yo \)

Los números complejos en forma exponencial se multiplican y dividen fácilmente. La potencia y raíz de números complejos en forma exponencial también se calculan fácilmente

Multiplicación de números complejos en formas exponenciales

Sean \( z_1 = r_1 e^{ i \theta_1} \) y \( z_2 = r_2 e^{ i \theta_2} \) números complejos en forma exponencial .
El producto de \( z_1 \) y \( z_2 \) viene dado por
\[ z_1 z_2 = r_1 r_2 e ^{ i (\theta_1+\theta_2) } \]

Ejemplo 3
Dado \( z_1 = 3 e^{ i \pi/4 } \) y \( z_2 = 5 e^{i 3\pi/4 } \)
Encuentra \( z_1 z_2\) y escríbelo en forma estándar.
Solución al ejemplo 3
\( z_1 z_2 = (3 e^{ i \pi/4 }) (5 e^{ i 3 \pi/4 } )\)
Multiplica los módulos \( 3 \) y \( 5 \) juntos y aplica la regla de los exponentes aplica la regla de los exponentes \( e^x e^y = e^{x+y} \)
\( = (3 \times 5) e^{ i\pi/4 + i 3\pi/4 } \)
Simplificar
\( = 15 e^{ i \pi } \)
Reescribir en forma polar
\( = 15 (\cos \pi + i \sin \pi) \)
Simplificar
\( = - 15 \)

Division of Complex Numbers in Exponential Forms

Let \( z_1 = r_1 e^{ i \theta_1} \) and \( z_2 = r_2 e^{ i \theta_2 } \) be complex numbers in exponential form .
The ratio (or division) of \( z_1 \) and \( z_2 \) is given by
\[ \dfrac{z_1}{ z_2} = \dfrac{r_1}{r_2} e ^{ i (\theta_1-\theta_2) } \]

Example 4
Given \( z_1 = 10 e^{ i \pi/3 } \) and \( z_2 = 2 e^{ i 2\pi/3 } \)
Find the product \( \dfrac{z_1}{z_2} \) and write it in standard form.
Solution to Example 4
\( \dfrac{z_1}{z_2} = \dfrac{10 e^{ i \pi/3 }} {2 e^{ i 2 \pi/3 } }\)
Divide the modulii \( 10 \) by \( 2 \) and apply the rule of exponents \( \dfrac{e^x}{e^y} = e^{x-y} \)
\( = \dfrac {10}{2} e^{ i ( \pi/3 - 2\pi/3 ) } \)
\( = 5 e^{ - i \pi/3 } \)
Rewrite in polar form
\( = 5 (\cos (- \pi/3) + i \sin (- \pi/3) ) \)
Simplify
\( = 5(1/2 - \dfrac{\sqrt 3}{2} i) = \dfrac{5}{2} - \dfrac{5\sqrt3}{2} i \)

You may also review De Moivre's Theorem Power and Root of Complex Numbers.

Questions

1) Write the following complex numbers in exponential forms .

\( z_1 = - 1 \)
\( z_2 = - 2 i \)
\( z_3 = -\sqrt3 - i \)
\( z_4 = - 3 + 3\sqrt 3 i \)
\( z_5 = 7 - 7 i \)

.

2) Use the results in part a) above to evaluate the following expressions and write them in exponential form .

\( z_4 z_5 \)
\( \dfrac{z_3 z_5}{z_4} \)

Solutions to the Above Questions

\( z_1 = -1 = e^{ i \pi} \)
\( z_2 = - 2 i = 2 e^{ i 3\pi/2 } \)
\( z_3 = -\sqrt3 - i = 2 e^{ i 7\pi/6}\)
\( z_4 = - 3 + 3\sqrt 3 i = 6 e^{ i 2\pi/3 } \)
\( z_5 = 7 - 7 i = 7 \sqrt 2 e^{ i 7\pi/4} \)

.

2)

\( z_4 z_5 = (6 e^{ i 2\pi/3 }) (7 \sqrt 2 e^{ i 7\pi/4}) \)
Use rule of multiplication given above
\( = 42 \sqrt 2 e^{i(2\pi/3 + 7\pi/4)} \)
Simplify
\( = 42 \sqrt 2 e^{i 29\pi/12} \)
Argument is larger than \( 2 \pi \) therefore you may subtract \( 2 \pi \) from it
\( = 42 \sqrt 2 e^{i (29\pi/12-2\pi )} \)
Simplify
\( = 42 \sqrt 2 e^{i 5\pi/12 } \)
\( \dfrac{z_3 z_5}{z_4} = \dfrac{( 2 e^{ i 7\pi/6})(7 \sqrt 2 e^{ i 7\pi/4})}{6 e^{ i 2\pi/3 }} \)
Use rule of multiplication and division given above
\( = \dfrac{2 \times 7 \sqrt 2}{6} e^{i(7\pi/6 + 7\pi/4 - 2\pi/3)} \)
Simplify
\( = \dfrac{7\sqrt{2}}{3} e^{i 9\pi/4} \)
Argument is larger than \( 2 \pi \) therefore you may subtract \( 2 \pi \) from it
\( = \dfrac{7\sqrt{2}}{3} e^{i (9\pi/4- 2\pi) } \)
Simplify
\( \dfrac{7\sqrt{2}}{3} e^{i \pi/4 } \)