Math Problems with Solutions for Grade 5
Grade 5 word problems and problems on patterns, time addition and subtraction, time-distance-speed, fractions and mixed numbers, ratios, percentages, and area and volume of rectangles and squares are presented. Each problem includes in-depth solutions and clear explanations. Some challenging problems are also included to stretch your thinking and build confidence.
Question 1
Sarah baked a cake and cut it into 8 equal slices. She ate 3 slices, and her friend Jake ate 1 slices. What fraction of the cake is left? Simplify the fraction if possible.
Total slices = 8
Slices eaten = 3 (Sarah) + 1 (Jake) = 4
Slices left = 8 - 4 = 4 \[ \text{The fraction left} = \dfrac{4}{8}\] Divide both numerator and denominator by 4: \[ \text{The fraction left} = \dfrac{4\div 4}{8\div 4}\] Simplify \[ \text{The fraction left} = \dfrac{ 1 }{2}\]
Question 2
A bookstore sells books for $15 each. If a customer buys 3 books and then gets a 25% discount on the total price, how much will the customer pay in total?
Total price before discount is: \[ 3 \times 15 = 45 \; \text{dollars } \] Total discount is: \[ 25\% \; \text{of} \; 45 = \dfrac{25}{100} \times 45 \] \[= 0.25 \times 45 = 11.25 \; \text{dollars } \] Total price after discount: \[ 45 - 11.25 = 33.75 \; \text{dollars } \] The customer will pay \$33.75.
Question 3
The first four numbers in a sequence are 3, 6, 12, 24. Explain the pattern and find the 7th number in the sequence?
The pattern starts with 3 and then each number is multiplied by 2 to get the next number.
1st: 3
2nd: \( 3 \times 2 = 6 \)
3rd: \( 6 \times 2 = 12 \)
4th: \( 12 \times 2 = 24 \)
5th: \( 24 \times 2 = 48 \)
6th: \( 48 \times 2 = 96 \)
7th: \( 96 \times 2 = 192 \)
The 7th number in the sequence is 192.
Question 4
It takes John 25 minutes to walk to the car park and 45 minutes to drive to work. At what time should he get out of the house in order to get to work at 9:00 a.m.?
The time it takes John to get to work is the sum of the time to walk to the car park and the time to drive: \[ \text{Total time} = 25 + 45 = 70 \text{ minutes} \] Since \( 70 \text{ minutes} = 60 \text{ minutes} + 10 \text{ minutes} \), and knowing that \( 1 \text{ hour} = 60 \text{ minutes} \), we can write: \[ \text{Total time} = 1 \text{ hour and } 10 \text{ minutes} \] John needs to leave the house 1 hour and 10 minutes before 9:00 a.m.: \[ 9:00 - 1:10 = 9:00 - 1:00 - 0:10 = 8 - 0:10 = 7:50 \text{ a.m.} \] John should leave the house at 7:50 a.m.
Question 5
Kim can walk \( 4 \) kilometers in one hour. How long does it take Kim to walk \( 18 \) kilometers?
If Kim walks \( 4 \) km in \( 1 \) hour, then the time to walk \( 18 \) km is: \[ \dfrac{18}{4} = 4.5 = 4 + \dfrac{1}{2} \] It takes Kim \( 4.5 \) hours (or 4 hours and 30 minutes) to walk 18 kilometers.
Question 6
A factory produced 2,300 TV sets in its first year of production. 4,500 sets were produced in its second year, and 500 more sets were produced in its third year than in its second year. How many TV sets were produced in three years?
500 TV sets were produced in the third year more than in the second year. Therefore, the number of sets produced in the third year is: \[ 4500 + 500 = 5000 \] The total number of TV sets produced in three years is: \[ 2300 + 4500 + 5000 = 11800 \] Conclusion: 11,800 TV sets were produced over 3 years.
Question 7
Tom and Bob have a total of 49 toys. If Bob has 5 more toys than Tom, how many toys does each one have?
If 5 toys are taken out of the 49 toys and the remaining ones are distributed equally between Tom and Bob, they will both have the same number of toys. \[ 49 - 5 = 44 \quad \text{(to be shared equally)} \] If distributed equally, each one will have: \[ \dfrac{44}{2} = 22 \quad \text{toys} \] Bob has 5 more toys than Tom, so Bob has: \[ 22 + 5 = 27 \quad \text{toys} \] Tom has 22 toys and Bob has 27 toys.
Note: check that the total is 49 and that Bob has 5 more toys than Tom.
Question 8
John can eat a quarter of a pizza in one minute. How long does it take John to eat one pizza and a half?
2 Possible Solutions:
1) There are 4 quarters in one whole pizza, and there are 2 quarters in half a pizza. So, in total, one pizza and a half has: \[ 4 + 2 = 6 \text{ quarters} \] If John eats one quarter in one minute, he needs: \[ 6 \times 1 = 6 \text{ minutes} \] to eat one pizza and a half.
2) The problem can also be solved using fractions:
One and a half pizzas is written as the mixed number: \[ 1\dfrac{1}{2} \] John needs one minute to eat one quarter. To find out how many quarters are in \(1\dfrac{1}{2}\), we divide: \[ 1\dfrac{1}{2} \div \dfrac{1}{4} \quad (1) \] Convert the mixed number to an improper fraction: \[ 1\dfrac{1}{2} = 1+ \dfrac{1}{2} = \dfrac{2}{2} + \dfrac{1}{2} = \dfrac{3}{2} \] Now perform the division (1) to find the number of quarters in \( 1\dfrac{1}{2} \): \[ \dfrac{3}{2} \div \dfrac{1}{4} = \dfrac{3}{2} \times \dfrac{4}{1} = \dfrac{12}{2} = 6 \] So there are 6 quarters in one and a half pizzas. Therefore, John needs: \[ 6 \times 1 = 6 \text{ minutes} \] to eat the entire pizza and a half.
Question 9
John read a quarter of the time that Tom read. Tom read only two-fifths of the time that Sasha read. Sasha read twice as long as Mike. If Mike read 5 hours, how long did John read?
Mike read 5 hours. Sasha read twice as long as Mike. Hence, Sasha read: \[ 2 \times 5 = 10 \text{ hours} \] Tom read two-fifths of the time that Sasha read. Hence, Tom read: \[ \dfrac{2}{5} \times 10 = 4 \text{ hours} \] John read a quarter of the time that Tom read. Hence, John read: \[ \dfrac{1}{4} \times 4 = 1 \text{ hour} \] Conclusion: John read for 1 hour.
Question 11
Jim, Carla and Tomy are members of the same family. Carla is 5 years older than Jim. Tomy is 6 years older than Carla. The sum of their three ages is 31 years. How old is each one them?
This problem can be solved using algebra or a table:
Algebra Method
Let \( x \) be Jim's age.
Carla is 5 years older than Jim, hence Carla's age is \[ x + 5 \] Tomy is 6 years older than Carla, hence Tomy's age is \[ x + 5 + 6 = x + 11 \]. The sum of all 3 ages is 31, hence: \[ x + ( x + 5 ) + (x+11) = 31 \] Group like terms \[ 3 x + 16 = 31 \] Subtract 16 from both sides of the equation and simplify: \[ 3 x = 15 \] Solve for x: \[ x = 5 \] Jim's age is: 5 , Carla's age is: 5 + 5 = 10 and Tomy's age is: 10 + 6 = 16.
Table Method
If if for reasons you cannot solve this problem using algebra, this problem can be solved using a table as shown below where Jim's age is guessed then Carla's and Tomy's ages are calculated. The calculations are stopped when the condition in the problem which is "the sum of their three ages is 31 years" is reached.
| Jim's age | Carla's age | Tomy's age | The sum of all ages |
|---|---|---|---|
| 1 | 1 + 5 = 6 | 6 + 6 = 12 | 1 + 6 + 12 = 19 |
| 2 | 2 + 5 =7 | 7 + 6 = 13 | 2+ 7 + 13 = 22 |
| 3 | 3 + 5 = 8 | 8 + 6 = 14 | 3 + 8 + 14 = 25 |
| 4 | 4 + 5 = 9 | 9 + 6 = 15 | 4 + 9 + 15 = 28 |
| 5 | 5 + 5 = 10 | 10 + 6 = 16 | 5 + 10 + 16 = 31 |
Question 12
Mel had \$35.00 and withdrew some more money from his bank account. He bought a pair of trousers at \$34.00, two shirts at \$16.00 each, and two pairs of shoes at \$24.00 each. After shopping, he had \$32.00 left. How much money did Mel withdraw from the bank?
Mel spent:
\$34.00 on a pair of trousers
\(2 \times 16.00 = \$32.00\) on two shirts (\$16.00 each)
\(2 \times 24.00 = \$48.00\) on two pairs of shoes (\$24.00 each)
The total amount of money spent by Mel is: \[ 34.00 + 32.00 + 48.00 = 114.00 \] He had \$32.00 left after shopping, so the total amount of money he had before shopping is: \[ 114.00 + 32.00 = 146.00 \] This total includes the \$35.00 he originally had, plus the amount he withdrew from the bank. Therefore, the amount he withdrew is: \[ 146.00 - 35.00 = 111.00 \] Mel withdrew \$111.00 from the bank.
Question 13
How many minutes are in one week?
1 week = 7 days
1 day = 24 hours
1 hour = 60 minutes
Hence in one week, there are:
\[ 7 \times 24 \times 60 = 10080 \; \text{minutes in one week} \]
Question 14
In Tim's house, a rectangular swimming pool (blue) whose length 30 meters and width 10 meters is surrounded by grass (green). The pool with the grassy area make a large rectangle whose length is 50 meters and width 20 meters. What area is occupied by the grass?
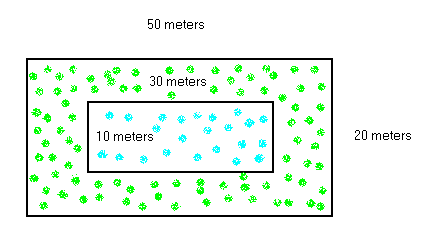 .
.
The area of a rectangle is calculated using the formula: \[ \text{Area} = \text{Length} \times \text{width} \] Area of the large rectangle (pool and grass) is: \[ 50 \times 20 = 1000 \; \text{metres squared} \] Area of the pool is: \[ 30 \times 10 = 300 \; \text{metres squared} \] \[ \text{Area of grass = Area of the large rectangle - Area of the pool} \] \[ = 1000 - 300 = 700 \; \text{metres squared} \]
Question 15
Mary wants to make a box. She starts with a piece of cardboard whose length is 15 centimeters and width is 10 centimeters. Then she cuts congruent squares with a side of 3 centimeters from each of the four corners. What is the area of the cardboard after she cuts the 4 corners?
The total area of the cardboard before cutting is: \[ \text{Area} = \text{Length} \times \text{Width} = 15 \times 10 = 150 \text{ cm}^2 \] Area of one square cut from a corner: \[ \text{Area of 1 square} = 3 \times 3 = 9 \text{ cm}^2 \] There are 4 such squares, so the total area cut out is: \[ 4 \times 9 = 36 \text{ cm}^2 \] Therefore, the area of the cardboard after cutting the 4 corners is: \[ 150 - 36 = 114 \text{ cm}^2 \]
Question 16
A painter charges \$225.00 for materials and \$35.00 per hour for labor. The total cost of painting an office is \$330.00. How many hours did it take the painter to paint the office?
When we subtract the cost of materials from the total cost, we get the total cost of labor: \[ 330.00 - 225.00 = 105.00 \] So \$105.00 is the total labor cost. Since the painter charges \$35.00 per hour, the number of hours is: \[ \dfrac{105.00}{35} = 3 \text{ hours} \]
Question 17
Three toy cars and 4 toy trains cost $18. Two toy cars and 3 toy trains cost $13. What is the price of one toy car and the price of one toy train if both prices are whole numbers of Dollars? (Hint: Use a table)
Use a table and guess the price of one toy car and one toy train then check the 2 conditions:
1) condition 1: Three toy cars and 4 toy trains should cost $18
2) condition 2: Two toy cars and 3 toy trains should cost $13
Note that as long as condition 1 is not satisfied, there no need to try to satisfy condition 2 because we need both of them to be statisfied at the same time.
The results in the table below shows that conditions 1 and 2 are satisfied when
price of 1 car is $2 and the price of a train is $3.
| Guess price of 1 car |
Guess price of 1 train |
Calculate Condition(1) 3 cars + 4 trains |
Calculate Condition(2) 2 cars + 3 trains |
|---|---|---|---|
| 1 | 1 | 3×1+4×1 = 7 | No need for calculations |
| 1 | 2 | 3×1+4×2 = 11 | No need for calculations |
| 1 | 3 | 3×1+4×3 = 15 | No need for calculations |
| 1 | 4 | 3×1+4×4 = 19 | No need for calculations |
| 2 | 1 | 3×2+4×1 = 10 | No need for calculations |
| 2 | 2 | 3×2+4×2 = 14 | No need for calculations |
| 2 | 3 | 3×2+4×3 = 18 | 2×2+3×3 = 13 |
Note that this problem can be solved algebraically as follows:
Let \( x \) be the cost of one toy car (in dollars)
Let \( y \) be the cost of one toy train (in dollars) The above statement is translated as:
1. Three toy cars and four toy trains cost $18: \[ 3x + 4y = 18 \] 2. **Two toy cars and three toy trains cost $13: \[ 2x + 3y = 13 \] So we end up with a system of equations: \[ \begin{cases} 3x + 4y = 18 \\ 2x + 3y = 13 \end{cases} \] Solve the system to obtain the price of one car \( x = \$2 \) and the price of one train \( y = \$3 \).
Question 18
A box has a length of 5 cm, a width of 3 cm, and a height of 4 cm. What is the volume of the box?
\[ \text{Volume = length } \times \text{width} \times \text{height} \] \[ = 5 \times 3 \times 4 = 60 \; \text{cubic centimeters} \] The volume of the box is 60 cm3.
Question 19
A bag contains 6 red balls, 4 blue balls, and 10 green balls. If a ball is picked at random, what is the probability that the ball will be blue? Write your answer as a fraction in simplest form.
Total number of balls is: \[ 6 + 4 + 10 = 20 \] Number of blue balls = 4
The probability of picking a blue ball is: \[ \dfrac{\text{ Number of blue balls }}{\text{Total number of balls}} = \dfrac{4}{20} = \dfrac{1}{5} \] The probability is \( \dfrac{1}{5} \).
Question 20
John bought 3.75 meters of fabric to make a curtain. He used 2.4 meters for one curtain and 0.85 meters for another. How much fabric does he have left?
Total fabric used ls: \[ 2.4 + 0.85 = 3.25 \; \text{ meters } \] Fabric left is: \[ 3.75 - 3.25 = 0.5 \; \text{ meters } \] John has 0.5 meters of fabric left.
Question 21
Linda spent \( \dfrac{3}{4} \) of her savings on furniture. She then spent \( \dfrac{1}{2} \) of her remaining savings on a fridge. If the fridge cost her $150, what were her original savings?
Let \( x \) be Linda's total savings. If she spent \( \dfrac{3}{4} \) of her savings on furniture, then \[ 1 - \dfrac{3}{4} = \dfrac{4}{4} - \dfrac{3}{4} = \dfrac{1}{4} \] of her savings remain, which can be expressed as: \[ \dfrac{1}{4} x \] She then spent \( \dfrac{1}{2} \) of her remaining savings on a fridge that costs $150. Therefore, we have the equation: \[ \dfrac{1}{2} \times \left( \dfrac{1}{4} x \right) = 150 \] Simplifying the above expression: \[ \dfrac{x}{8} = 150 \] Now, multiply both sides of the equation by 8 to solve for \( x \): \[ 8 \times \left( \dfrac{x}{8} \right) = 8 \times 150 \] \[ x = 1200 \] Linda's original savings were $1200.
Question 22
The perimeter of square A is 3 times the perimeter of square B. What is the ratio of the area of square A to the area of square B.
Let \( x \) be the length of the side of square A and \( y \) be the length of the side of square B.
The perimeters of the two squares are given by:
Perimeter of square A: \[ 4x \] Perimeter of square B: \[ 4y \] The expression "The perimeter of square A is 3 times the perimeter of square B" is written mathematically as: \[ 4x = 3(4y) = 12y \] Divide left and right sides by 4: \[ x = 3y \] Square both sides of the equation: \[ x^2 = (3y)^2 \] Simplify: \[ x^2 = 9y^2 \] The areas of the two squares are:
Area of square A: \[ x^2 \] Area of square B: \[ y^2 \] The ratio of the area of square A to the area of square B is: \[ \dfrac{x^2}{y^2} \] Using the equation \( x^2 = 9y^2 \), divide both sides by \( y^2 \): \[ \dfrac{x^2}{y^2} = \dfrac{9y^2}{y^2} \] Simplify: \[ \dfrac{x^2}{y^2} = 9 \] The ratio of the area of square A to the area of square B is \( 9:1 \).
Question 23
Mary wants to make an open rectangular box. She starts with a piece of cardboard whose length is 15 centimeters and width is 10 centimeters. Then she cuts 4 congruent squares with sides of 3 centimeters at the four corners and folded at the broken lines to make the box. What is the volume of the box?
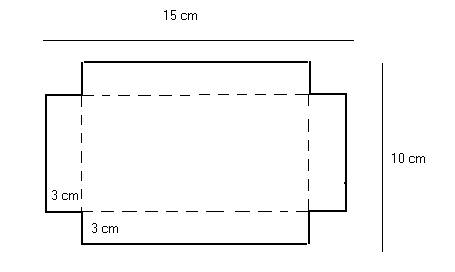 .
.
The length of the box is given by (subtract 3 cm twice): \[ 15 - 3 - 3 = 9 \text{ cm} \] The width of the box is given by (subtract 3 cm twice): \[ 10 - 3 - 3 = 4 \text{ cm} \] The height of the box, after folding, is equal to \[ 3 \text{ cm} \] The din=mensions of the open rectangular box are: length = 9, width = 4 and height = 3.
Hence, the volume \( V \) of the open rectangular box is given by \[ V = \text{length} \times \text{width} \times \text{height} = 9 \times 4 \times 3 = 108 \text{ cm}^3 \]
Question 24
A small square of side \( 2x \) is cut from one corner of a rectangle whose is width is 10 centimeters and length 20 centimeters. Write an expression in terms of \( x \) for the area of the remaining shape.
Let us first find the total area \( A \) of the rectangle before the square is cut: \[ A = \text{length} \times \text{width} = 20 \times 10 = 200 \] A square of side \( 2x \) has an area \( B \) given by: \[ B = (2x) \times (2x) = 4x^2 \] The small square of area \( B \) is cut from the large rectangle of area \( A \). Hence, the area of the remaining shape is: \[ A - B = 200 - 4x^2 \]
Question 25
The coordinates of point A are (2, 3), and the coordinates of point B are (6, 7). What is the \( d \) distance between points A and B? (Use the distance formula: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Using the distance formula: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \] Let \( A = (x_1 - y_1) = (3, 8) \) and \( B = (x_2 - y_2) = (11, 2) \) and substitute in the formula given above. \[ d = \sqrt{ (11 - 3)^2 + (2 - 8)^2 } \] \[= \sqrt{ 8^2 + (-6)^2} \] \[ = \sqrt{64 + 36} = \sqrt{100} \] \[ d = \sqrt{100} = 10 \; \text{units} \] The distance between points A and B is 10 units.