Find Equation of a Line from a Graph

Examples on how to find the equations of lines given their graphs. Examples and exercises are presented along with their detailed solutions and answers.
These following are reviews of formulas for slopes and equations of lines and are therefore used to solve the examples below.

1. The slope $m$ of a line with rise $\Delta y$ corresponding to a run $\Delta x$ is given by $$m = \dfrac{\Delta y }{\Delta x}$$
2. The slope $m$ of a line through two points with coordinates $(x_1,y_1)$ and $(x_2,y_2)$ is given by $$m = \dfrac{y_2 - y_1}{x_2 - x_1}$$
3. The equation of a line that passes through the point $(y_0 , x_0)$ and has slope $m$ is given by $$y - y_0 = m(x - x_0)$$
4. The equation of a line with the y - intercept at $(0 , b)$ and has slope $m$ is given by $$y = m x + b$$
5. The equation of a horizontal line through the point $(x_0 , y_0)$ is given by $$y = y_0$$
6. The equation of a vertical line through the point $(x_0 , y_0)$ is given by $$x = x_0$$
7. The slopes $m_1$ and $m_2$ of two perpendicular lines are related as follows $$m_1 \cdot m_2 = -1$$
8. The slopes $m_1$ and $m_2$ of two parallel lines are related as follows $$m_1 = m_2$$

Examples with Detailed Solutions

Example 1 Graph of line with points
Find the equation of the line whose graph is shown below and write it in slope intercept form.



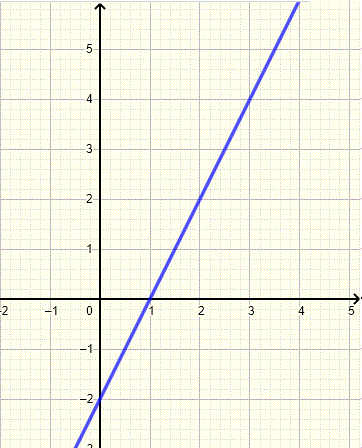
Solution to Example 1
Let use two points $(2,2)$ and $(3,4)$ from the graph to find the slope $m$ of the line whose graph is shown above
$m = \dfrac{4-2}{3-2} = 2$
We know at least a point and the slope, the equation of the line in point slope form is given by
$y - 2 = 2 (x - 2)$
In point slope form the equation is written as
$y = 2x - 2$

Example 2 Graph of line given run and rise
Find the equation of the line whose graph, including the rise and run, is shown below.



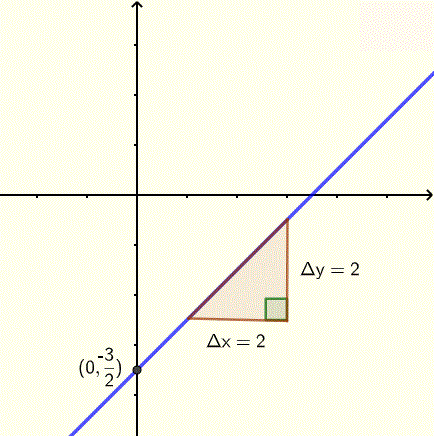
Solution to Example 2
The slope of the line whose graph is shown above is given by
$m = \dfrac{rise}{run} = \dfrac{\Delta y}{\Delta x} = \dfrac{2}{2} = 1$
The y intercept is the point $(0, - 3/2)$
The equation of the line in slope intercept form is given by
$y = x - 3/2$

Example 3 Graph of line given run and fall
Find the equation, in slope intercept form, of the line whose graph, including the fall and run, is shown below.



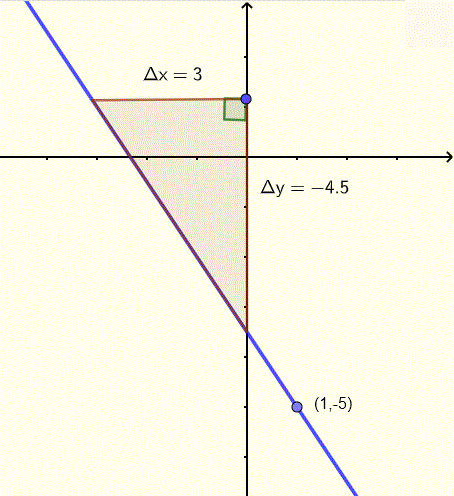
Solution to Example 3
The slope of the line whose graph is shown above is given by
$m = \dfrac{fall}{run} = \dfrac{\Delta y}{\Delta x} = \dfrac{-4.5}{3} = -1.5$
Given a point $(1,-5)$ and the slope of the line, we use the point slope form of the equation of the line
$y - (-5) = -1.5(x - 1)$
In slope intercept form, the equation of the above graph is written as
$y = -1.5 x - 3.5$

Example 4 Graph of horizontal line
Find the equation of the horizontal line whose graph is shown below.



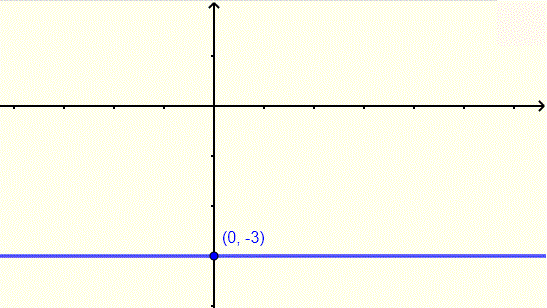
Solution to Example 4
The equation of the horizontal line through the point $(0,-3)$ is given by
$y = - 3$

Example 5 Graph of vertical line
Find the equation of the vertical line whose graph is shown below.



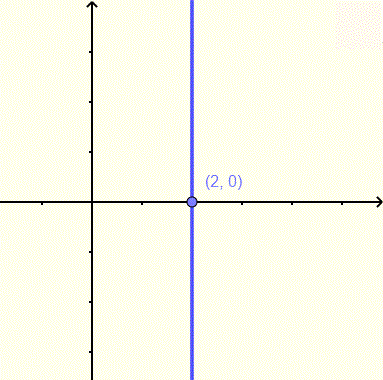
Solution to Example 5
The equation of the vertical line through the point $(2,0)$ is given by
$x = 2$

Example 6 Graph of perpendicular line
Find the slope intercept form of the equation of line $L_2$ that is perpendicular to line $L_1$ as shown below.



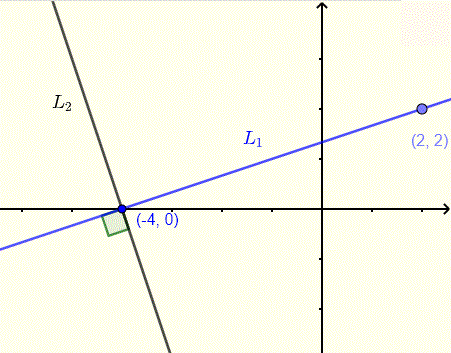
Solution to Example 6
We need to find the slope $m_2$ of line $L_2$ which is perpendicular to line $L_1$ with slope $m_1$ given by
$m_1 = \dfrac{2 - 0}{2 - (-4)} = \dfrac{1}{3}$
$L_1$ and $L_2$ are perpendicular and therefore
$m_1 \cdot m_2 = -1$
Solve the above for $m_2$
$m_2 = - 1 / m_1 = - 1 / (1/3) = - 3$
The equation of line $L_1$ in point slope form is given by
$y - 0 = - 3(x - (-4))$
and in slope intercept form is given by
$y = - 3 x - 12$

Exercises with Answers

Find the equations of the lines $L_1$, $L_2$, $L_3$ and $L_4$ such that $L_2$ is parallel to $L_1$, $L_3$ is perpendicular to $L_1$ and $L_4$ is a horizontal line.



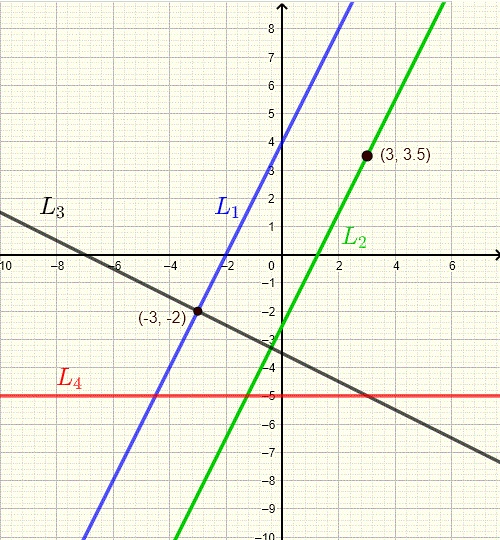
Answers to the Above Exercises

1. Equation of $L_1$ : $y = 2 x + 4$
2. Equation of $L_2$ : $y = 2x - 2.5$
3. Equation of $L_3$ : $y = - \dfrac{1}{2} x - \dfrac{7}{2}$
4. Equation of $L_4$ : $y = - 5$

More References and Links to Equations and Slopes of Lines