Scalar and Cross Products of 3D Vectors

The scalar (or dot product) and cross product of 3 D vectors are defined and their properties discussed and used to solve 3D problems.

Scalar (or dot) Product of Two Vectors

The scalar (or dot) product of two vectors \( \vec{u} \) and \( \vec{v} \) is a scalar quantity defined by:

\( \vec{u} \cdot \vec{v} = || \vec{u} || \, || \vec{v} || \cos \theta\)

where \( || \vec{u} || \) is the magnitude of vector \( \vec{u} \), \( || \vec{v} || \) is the magnitude of vector \( \vec{v} \) and \( \theta \) is the angle between the vectors \( \vec{u} \) and \( \vec{v} \).
If the components of vectors \( \vec{u} \) and \( \vec{v} \) are known: \( \vec{u} = (u_x , u_y ,u_z)\) and \( \vec{v} = (v_x , v_y , v_z) \), it can be shown that the scalar product may be expressed as follows:
\( \vec{u} \cdot \vec{v} = u_x v_x + u_y v_y + u_zv_z \)

Theorems on Scalar Products

If \( \vec{u} \), \( \vec{v} \) and \( \vec{w} \) are vectors and k is a scalar, then
1) \( \vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{u} \)
2) \( \vec{u} \cdot (\ \vec{v} + \vec{w} ) = \vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w} \)
3) \( \vec{u} \cdot \vec{u} = ||\vec{u} ||^2 \)
4) \( \vec{u} \cdot \vec{v} = 0 \; \) if and only if \( \; \theta = \pi/2 \), if both \( \vec{u} \) and \( \vec{v} \) are non zero vectors.
5) \( (k \vec{u}) \cdot \vec{v} = \vec{u} \cdot ( k\vec{v}) = k ( \vec{u} \cdot \vec{v} ) \)
6) \(|\vec{u} \cdot \vec{v} | \le ||\vec{u}|| ||\vec{v}|| \)
7) \(||\vec{u} + \vec{v} || \le ||\vec{u}|| + ||\vec{v}|| \)

Example 1

Approximate, to the nearest degree, the angle between the vectors \(\vec{v}=<-2,3,1> \text{and} \vec{u}= <0,-1,4>\).

solution


Express the scalar product of the two vectors using the magnitude and angle \( \theta \) between them and the coordinates as follows:
\(\vec{v} \cdot \vec{u} = ||\vec{v} || || \vec{u} || cos \theta = (-2)(0) + (3)(-1) + (1)(4) = 1 \)
\( ||\vec{v} || = \sqrt{(-2)^2+3^2+1^2} = \sqrt{14}\)
\( ||\vec{u} || = \sqrt{0^2+(-1)^2+4^2} = \sqrt{17} \)
\( cos\theta = \dfrac{1}{||\vec{v} || || \vec{u} ||} = \dfrac{1}{\sqrt{14}\sqrt{17}} \)
\( \theta = \arccos(\dfrac{1}{\sqrt{14}\sqrt{17}} ) \approx 86^{\circ}\)

More explanations on finding the angle between vectors on a video.

Example 2

Find \( a \) so that the vectors \( \lt a,-6,3 \gt \) and \( <1,0,-2> \) are perpendicular.

solution


For two vectors to be perpendicular, their scalar product must be equal to zero.
\( \lt a,-6,3 \gt \cdot <1,0,-2> = a(1) + (-6)(0)+(3)(-2) = a - 6 = 0 \)
Solve for a
\( a = 6\)

Scalar and Vector Projection of a Vector onto Another

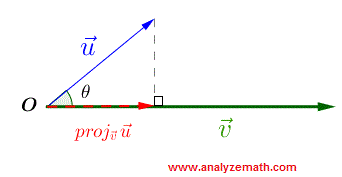
In many applications, it is important to find the component of a vector in the direction of another vector. As shown below, vector \( \vec{u}\) is projected onto vector \( \vec{v}\) by dropping a perpendicular from the terminal point of \( \vec{u}\) to the line through \( \vec{v}\). The component of \( \vec{u}\) along \( \vec{v}\) is a scalar quantity called the scalar projection and is given by

\( \text{comp}_{\vec{v}}\vec{u} = ||\vec{u}|| \cos \theta \)
.
The vector projection of \( \vec{u}\) on \( \vec{v}\) is a vector quantity obtained by multiplying the component \( \text{comp}_{\vec{v}}\vec{u} \) by the unit vector in the direction of vector \( \vec{v}\) and is given by
\( \text{proj}_{\vec{v}}\vec{u} = ||\vec{u}|| \cos \theta \dfrac{\vec{v}}{||\vec{v}||} = \dfrac{\vec{u}\cdot\vec{v}}{||v||^2} \vec{v}\)
.

vector projection on another vector

Cross (or vector) Product of Two Vectors

The cross (or vector) product of two vectors \( \vec{u} = (u_x , u_y ,u_z)\) and \( \vec{v} = (v_x , v_y , v_z) \) is a vector quantity defined by:

\( \vec{u} \times \vec{v} = {\begin{vmatrix}\vec{i}& \vec{j} &\vec{k} \\ u_x & u_y & u_z \\ v_x & v_y & v_z \end{vmatrix}} = {\begin{vmatrix} u_y & u_z \\ v_y & v_z \end{vmatrix}} \vec{i} - {\begin{vmatrix}u_x & u_z\\ v_x & v_z\end{vmatrix}} \vec{j} + {\begin{vmatrix}u_x & u_y\\ v_x & v_y\end{vmatrix}} \vec{k}\)

 The cross product \( \vec{u} \times \vec{v} \) is perpendicular to both \( \vec{v} \) and \( \vec{u} \)

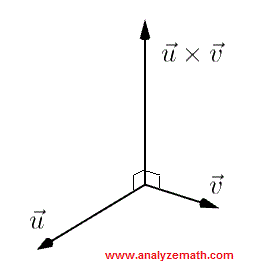cross product of two vectors


The right hand rule, to find the direction of the cross product, is as follows: point the index in the direction of \( \vec {u} \), the middle finger in the direction of \( \vec{v} \) and the direction of the cross product \( \vec {u} \times \vec {v} \) is in the same direction as that of the thumb.

right hand rule

Theorems on Cross Products

If \( \vec{u} \), \( \vec{v} \) and \( \vec{w} \) are vectors and k is a scalar, then
1) The cross product \( \vec{u} \times \vec{v} \) is perpendicular to both \( \vec{v} \) and \( \vec{u} \)
2) \( \vec{u} \times \vec{v} = - \vec{v} \times \vec{u} \)
3) \( \vec{u} \times \vec{v} = 0 \) if and only if \( \vec{u} \) and \( \vec{v} \) are parallel , if both \( \vec{u} \) and \( \vec{v} \) are non zero vectors.
4) \( \vec{u} \times (\ \vec{v} + \vec{w} ) = \vec{v} \times \vec{u} + \vec{u} \times \vec{w} \)
5) \( (k \vec{u}) \times \vec{v} = \vec{u} \times ( k\vec{v}) = k ( \vec{u} \times \vec{v} ) \)
6) \( ||\vec{u} \times \vec{v} || = ||\vec{u}|| ||\vec{v}|| sin \theta\) , where \( \theta \) is the angle between \( \vec{u}\) and \( \vec{v} \).

Area of a Parallelogram

A parallelogram is a quadrilateral (4 sides) with opposite sides parallel. In the figure below is shown the parallelogram A, B, C and D. Hence, we have equality between the vectors.
\( \vec{AB} = \vec{DC} \) and \( \vec{AD} = \vec{BC} \)
The area of the parallelagram is given by \( || \vec{AB} \times \vec{AD} || \)

definition of parallelogram and the formula of its area


The area of a triangle may be calculated as half the area the corresponding parallelogram.

Volume of a Parallelepiped

A parallelepiped is a 3d figure formed by 6 parallelograms as shown in the figure below. We have equality between several vectors.
\( \vec{AE} = \vec{DH} = \vec{CG} = \vec{BF} = \vec{u} \)
\( \vec{AD} = \vec{BC} = \vec{EH} = \vec{FG} = \vec{v}\)
\( \vec{AB} = \vec{DC} = \vec{EF} = \vec{HG} = \vec{w}\)
The volume V of the parallelepiped is given by
V \( = |\vec{u}\cdot (\vec{v} \times \vec{w})| = | \vec{v}\cdot (\vec{w} \times \vec{u})| = | \vec{w}\cdot (\vec{v} \times \vec{u})| \)

definition of parallelepiped and the formula of its volume

Example 3

Calculate the cross product of the vectors \(\vec{u} = <1,1,3>\) and \(\vec{v} = <1,0,2>\).

A video on how to find the Cross Product of Two Vectors with detailed explanations.

solution
\( \vec{u} \times \vec{v} = {\begin{vmatrix}\vec{i}& \vec{j} &\vec{k} \\ 1 & 1 & 3 \\ 1 & 0 & 2 \end{vmatrix}} = {\begin{vmatrix} 1 & 3 \\ 0 & 2 \end{vmatrix}} \vec{i} - {\begin{vmatrix}1 & 3\\ 1 & 2\end{vmatrix}} \vec{j} + {\begin{vmatrix}1 & 1\\ 1& 0\end{vmatrix}} \vec{k} = 2\vec{i} + \vec{j} -\vec{k} \)

Example 4

Find two unit vectors perpendicular to the vectors \( \vec{u} = \lt 1,-2,1 \gt \) and \( \vec{v} = <-2,0,4> \).

solution


The cross product \( \vec{w} = \vec{u} \times \vec{v} \) is a vector perpendicular to both vectors \( \vec{u} \; \text{and} \; \vec{v} \).
Let us calculte \( \vec{u} \times \vec{v} \) as follows:
\( \vec{w} = \vec{u} \times \vec{v} = {\begin{vmatrix}\vec{i}& \vec{j} &\vec{k} \\ 1 & -2 & 1 \\ -2 & 0 & 4 \end{vmatrix}} = {\begin{vmatrix} -2 & 1 \\ 0 & 4 \end{vmatrix}} \vec{i} - {\begin{vmatrix}1 & 1\\ -2 & 4\end{vmatrix}} \vec{j} + {\begin{vmatrix}1 & -2\\ -2 & 0\end{vmatrix}} \vec{k} = -8\vec{i} - 6 \vec{j} - 4 \vec{k} \)

We now need to find a unit vector \( \vec{u_1} \) in the same direction as \( \vec{w} \) and is given by
\( \vec{u_1} = \dfrac{1}{||\vec{w}||} \vec{w}\)
and a second unit vector \( \vec{u_2} \) in the opposite direction of \( \vec{w} \) and is given by
\( \vec{u_2} = -\vec{u_1}\)
\( ||\vec{w}|| = \sqrt{(-8)^2+(- 6)^2+(- 4)^2 } = 2\sqrt{29}\)
\( \vec{u_1} = \dfrac{1}{2\sqrt{29}} (-8\vec{i} - 6 \vec{j} - 4 \vec{k}) = -\dfrac{4}{\sqrt{29}}\vec{i} -\dfrac{3}{\sqrt{29}}\vec{j}-\dfrac{2}{\sqrt{29}}\vec{k}\)
\( \vec{u_2} = \dfrac{4}{\sqrt{29}}\vec{i} + \dfrac{3}{\sqrt{29}}\vec{j}+ \dfrac{2}{\sqrt{29}}\vec{k}\)

Example 5

Explain why the following statement are not true.
a) \( \vec{u} \times \vec{u} = ||\vec{u}||^2\)
b) \( \vec{u} \cdot (\vec{u} \times \vec{w} )= (\vec{u} \cdot \vec{u}) \times \vec{w} \)

solution


a) The left side \( \vec{u} \times \vec{u} \) is a cross product and the result is a vector. The right side \( ||\vec{u}||^2\) is a scalar quantity. A vector and a scalar cannot be compared.
b) The left side \( \vec{u} \cdot (\vec{u} \times \vec{w} ) \) is a scalar product of \( \vec{u} \) and \( (\vec{u} \times \vec{w} ) \) and the result is a scalar. The right side is the product of a scalar quantity \( \vec{u} \cdot \vec{u} \) and vector \( \vec{w} \) and the result is a vector. A scalar and a vector cannot be compared.

Answer the following Questions

Detailed Solutions and explanations to these questions.
1) Calculate \( \vec{u} \cdot (\vec{u} \times \vec{v}) \) given that \( \vec{u} = \lt a,b,c \gt \) and \( \vec{v} = \lt d,e,f \gt \).
2) Find \( k \) so that vectors \( \vec{u} = \lt -2,-k,1 \gt \) and \( \vec{v} = <8,-2,-3> \) are perpendicular
3)Find \( k \) so that the vectors \( \vec{u} = \lt -3,2,-2 \gt \), \( \vec{v} = <2,1,k> \) and \( \vec{w} = <-1,3,-5> \) are on the same plane (or coplanar)?
4) Find angle \( \theta \) between the vectors \( \vec{u} = \lt 2,0,1 \gt \) and \( \vec{v} = <8,-2,-3> \).
5) Find the vector projection of \( \vec{u} = \lt -1,-1,1 \gt \) onto \( \vec{v} = <2,1,1> \).
6) Find that \( k \) so that the points \( A(-1,2,k) \), \( B(-3,6,3) \) and \( C(1,3,6) \) are the vertices of a right triangle with a right angle at \( A \).
7) Given vector \( \vec{v} = \lt 3,-1,-2 \gt \), find the vector \( \vec{u} \) such that \( \vec{v} \times \vec{u} = <4,2,5> \) and \( ||\vec{u}|| = 3\))
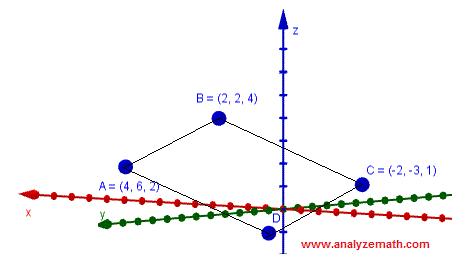
8) Points A, B, C and D forms a parallelogram.
a)Find the coordinates of point D.
b)Find the area of a parallelogram.

parallelogram in 3d


9) In the cube below find the angle between the diagonals AG and BH.

cube


10) Find a vector that is orthogonal to the plane containing the points A(1,2,-3), B(0,-2,1) and C(-2,0,1).
11) Find the area of the triangle whose vertices are the points A(1,0,-3), B(1,-2,0) and C(0,2,1).
12)Find the volume of the parallelepiped shown below.

volume of parallelepiped defined by points


Detailed Solutions and explanations to these questions.

More References and links

Cross Product of 3D Vectors
Cross Product of Two Vectors - Calculator
Dot Product of Two Vectors and Applications
Middle School Maths (Grades 6, 7, 8, 9) - Free Questions and Problems With Answers
Home Page