Grade 12 Math Problems with Solutions and Answers
Grade 12 math problems with detailed solutions are presented. More grade 12 math practice test are included in this website.
Free Practice for SAT, ACT
and Compass Math tests
-
Two large and 1 small pumps can fill a swimming pool in 4 hours. One large and 3 small pumps can also fill the same swimming pool in 4 hours. How many hours will it take 4 large and 4 small pumps to fill the swimming pool.(We assume that all large pumps are similar and all small pumps are also similar.)
-
Find all sides of a right triangle whose perimeter is equal to 60 cm and its area is equal to 150 square cm.
-
A circle of center (-3 , -2) passes through the points (0 , -6) and (a , 0). Find a.
-
Find the equation of the tangent at ( 0 , 2) to the circle with equation
(x + 2)2 + (y + 1)2 = 13
-
An examination consists of three parts. In part A, a student must answer 2 of 3 questions. In part B, a student must answer 6 of 8 questions and in part C, a student must answer all questions. How many choices of questions does the student have?
-
Solve for x
x 2 - 3|x - 2| - 4x = - 6
-
The right triangle ABC shown below is inscribed inside a parabola. Point B is also the maximum point of the parabola (vertex) and point C is the x intercept of the parabola. If the equation of the parabola is given by y = -x2 + 4x + C, find C so that the area of the triangle ABC is equal to 32 square units.
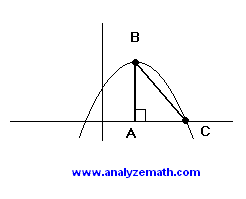 .
.
-
The triangle bounded by the lines y = 0, y = 2x and y = -0.5x + k, with k positive, is equal to 80 square units. Find k.
-
A parabola has two x intercepts at (-2 , 0) and (3 , 0) and passes through the point (5 , 10). Find the equation of this parabola.
-
When the polynomial P(x) = x3 + 3x2 -2Ax + 3, where A is a constant, is divided by x2 + 1 we get a remainder equal to -5x. Find A.
-
When divided by x - 1, the polynomial P(x) = x5 + 2x3 +Ax + B, where A and B are constants, the remainder is equal to 2. When P(x) is divided by x + 3, the remainder is equal -314. Find A and B.
-
Find all points of intersections of the 2 circles defined by the equations
(x - 2)2 + (y - 2)2 = 4
(x - 1)2 + (y - 1)2 = 4
-
If 200 is added to a positive integer I, the result is a square number. If 276 is added to to the same integer I, another square number is obtained. Find I.
-
The sum of the first three terms of a geometric sequence is equal to 42. The sum of the squares of the same terms is equal to 1092. Find the three terms of the sequence.
-
A rock is dropped into a water well and it travels approximately 16 t2 feet in t seconds. If the splash is heard 3.5 seconds later and the speed of sound is 1087 feet/second, what is the height of the well?
-
Two boats on opposite banks of a river start moving towards each other. They first pass each other 1400 meters from one bank. They each continue to the opposite bank, immediately turn around and start back to the other bank. When they pass each other a second time, they are 600 meters from the other bank. We assume that each boat travels at a constant speed all along the journey. Find the width of the river?
-
Find the constants a and b so that all the 4 lines whose equation are given by

.
pass through the same point.
-
Find the area of the right triangle shown below.

.
-
It takes pump A 2 hours less time that pump B to empty a swimming pool. Pump A is started at 8:00 a.m. and pump B is started at 10:00 a.m. At 12:00 p.m. 60% of the pool is empty when pump B broke down. How much time after 12:00 p.m. would it take pump A to empty the pool?
-
The number of pupils in school A is equal to half the number of pupils in school B. The ratio of the boys in school A and the boys in school B is 1:3 and the ratio of the girls in school A and the girls in school B is 3:5. The number of boys in school B is 200 higher than the number of boys in school A. Find the number of boys and girls in each school.
-
Four large and 2 small pumps can fill a swimming pool in 2 hours. Two large and 6 small pumps can also fill the same swimming pool in 2 hours. How long does it take 8 large and 8 small pumps to fill 50% of the swimming pool. (NOTE: all the large pump have same power and all the small pumps have the same power).
Solutions to the Above Problems
-
Let R and r the rate of work of the large and the small pumps respectively
4(2R + r) = 1 : 2 large and 1 small work for 4 hours to do 1 job
4(R + 3r) = 1 : 1 large and 3 small work for 4 hours to do 1 job
T(4R + 4r) = 1 : Find time T if 4 large and 4 small are to do one job.
Solve for R and r the system of first two equations then substitute in the third and solve for T to find the time. T = 5/3 hours = 1 hour 40 minutes.
-
x + y + H = 60 : perimeter , x, y and H be the two legs and the hypotenuse of the right triangle
(1/2)xy = 150 : area
x2 + y2 = H2: Pythagora's theorem.
3 equations with 3 unknowns.
(x + y)2 - 2xy = H2 : completing the square in the third equation.
x + y = 60 - H : express x + y using the first equation and use the second equation to find xy = 300 and substitute in equation 5.
(60 - H)2 - 600 = H2 : one equation with one unknown.
Solve for H to find H = 25 cm. Substitute and solve for x and y to find x = 15 cm and y = 20 cm.
-
√((-6 + 2)2 + (0 + 3)2) = √((a + 3)2 + (0 + 2)2) : distances from center to any point on the circle are equal.
(25) = (a + 3)2 + 4 : Simplify and square both sides
(a + 3)2 = 21 : Rewrite the above equation as
Solve for a
a = -3 + √(21) , a = -3 - √(21) : solve for a and find two solutions.
-
(-2 , -1) : center of circle
m = (2 - -1) / (0 - -2) = 3 / 2 : slope of line through the center and the point of tangency (0 , 2)
The line through the center and the point of tangency (0 , 2) is perpendicular to the tangent.
M = -2 / 3 : slope of tangent
y = -(2/3)x + 2 : equation of tangent given its slope and point (0 , 2).
-
3C2 × 8C6 × 1 = 84 : Use of fundamental theorem of counting
-
x2 - 3|x - 2| - 4x = - 6 : given
Let Y = x - 2 which gives x = Y + 2
(Y + 2)2 - 3|Y| - 4(Y + 2) = - 6 : substitute in above equation
Y2 - 3|Y| + 2 = 0
Y2 = |Y|2 : note
|Y|2 - 3|Y| + 2 = 0 : rewrite equation as
(|Y| - 2)(|Y| - 1) = 0
|Y| = 2 , |Y| = 1 : solve for |Y|
Y = 2, -2 , 1 , -1 : solve for Y
x = 4 , 0 , 3 , 1 : solve for x using x = Y + 2.
-
h = -b / 2a = 2 : x coordinate of the vertex of the parabola
k = -(2)2 + 4(2) + C = 4 + C : y coordinate of vertex
x = (2 + √(4 + C)) , x = (2 - √(4 + C)) : the two x intercepts of the parabola.
length of BA = k = 4 + C
length of AC = 2 + √(4 + C) - 2 = √(4 + C)
area = (1/2)BA × AC = (1/2) (4 + C) × √(4 + C)
(1/2) (4 + C) × √(4 + C) = 32 : area is equal to 32
C = 12 : solve above for C.
-
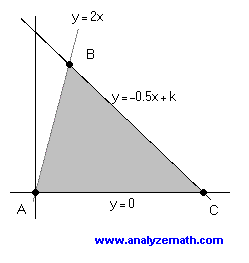
A(0,0) , B(2k/5 , 4k/5) , C(2k ,0) : points of intersection of the 3 points of intersection of the 3 lines
(1/2) × (4k/5) × (2k) = 80 : area given
k = 10 : solve the above equation for k , k positive is a given condition.
-
y = a(x + 2)(x - 3) : equation of the parabola in factored form
10 = a(5 + 2)(5 - 2) : (5 , 10) is a point on the graph of the parabola and therefore satisfies the equation of the parabola.
a = 5/7: solve the above equation for a.
-
Divide x3 + 3x2 -2Ax + 3 by (x2 + 1) to obtain a remainder = -x(1 + 2A)
-x(1 + 2A) = 5x : remainder given
-(1 + 2A) = 5 : polynomials are equal if they corresponding coefficient area equal.
A = -3 : Solve the above for A.
-
P(1) = 15 + 2(13) +A × (1) + B = 2 : remainder theorem
P(-3) = (-3)5 + 2(-3)3 +A × (-3) + B = -314
A = 4 and B = -5 : solve the above systems of equations.
-
x2 - 4x + 2 + y2 - 4y + 2 = 4 : expand equation of first circle
x2 - 2x + 1 + y2 - 2y + 1 = 4 : expand equation of second circle
-2x - 2y - 6 = 0 : subtract the left and right terms of the above equations
y = 3 - x : solve the above for y.
2x2 - 6x + 1 = 0 : substitute y by 3 - x in the first equation, expand and group like terms.
(3/2 + √(7)/2 , 3/2 - √(7)/2) , (3/2 - √(7)/2 , 3/2 + √(7)/2) : solve the above for x and use y = 3 - x to find y.
-
I + 200 = A2 : 200 added to I (unknown integer) gives a square.
I + 276 = B2 : 276 added to I (unknown integer) gives another square.
B2 = A2 + 76 : eliminate I from the two equations.
add squares A2 (0, 1, 4, 9, 16, 25,...) to 76 till you obtain another square B2.
76 + 182 = 400 = 202
A2 = 182 and B2 = 202
I = A2 - 200 = 124
-
sum1 = a + a r + a r2 = 42: the sum of the three terms given, r is the common ratio.
sum2 = a2 + a2r2 + ar2r4 = 1092: the sum of the squares of the three terms given .
sum1 = a + ar + ar2 = a(r3 - 1) / (r - 1) = 42 : apply formula for a finite sum of geometric series.
sum2 = a2 + a2r2 + ar2r4 = a2(r6 - 1) / (r2 - 1) = 1092: the sum of squares is a also a sum of geometric series.
sum2/sum12 = 1092 / 422 = [ a2(r6 - 1)/(r2 - 1)] / [a2(r3 - 1)2 / (r - 1)2]
(r2 - r + 1) / (r2 + r + 1) = 1092 / 422
r = 4 , r = 1/4 : solve for r
a = 2 : substitute r = 4 and solve for a
a = 32 : substitute r = 1/4 and solve for a
a = 2 , ar = 8 , ar2 = 32 : find the three terms for r = 4
a = 32 , ar = 8 , ar2 = 2 : find the three terms for r = 1/4
-
T1 + T2 = 3.5 : T1 time for the rock to reach bottom of well and T2 time for the sound to reach the top of the well.
16 × T12 = 1087 × T2 : same distance which the height of the well.
T2 = 3.5 - T1 : solve for T2
16 × T12 = 1087 × (3.5 - T1)
T1 = 3.34 seconds
Height = 16 × (3.34)2 = 178 feet (to the nearest unit)
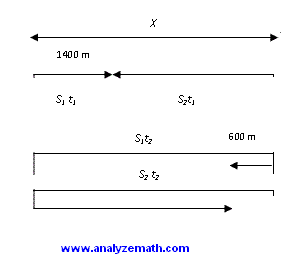 .
.
S1×t1 = 1400 : S1 speed of boat 1, t1 : time to do 1400 meters(boat 1)
1400 + S2×t1 = X : S2 speed of boat 2
S1×t2 = X + 600 : t2 time to do X + 600 (boat 2)
S2×t2 = 2X - 600
S1 = 1400/t1
S2 = (X-1400)/t1
T = t2/t1 : definition
substitute S1, S2 and t2/t1 using the above expressions in equations 3 and 4 to obtain
1400×T = X + 600
X×T - 1400×T = 2X - 600 : 2 equations 2 unknowns
Eliminate T and solve for X to obtain X = 3600 meters.
-
solve the system of the first two equations to obtain the solution (2 , -3)
The above solution is also a solution to the last two equations.
a(2) + b(-3) = 4
2a(2) - b(-3) = 2
a = 1 and b = -2/3 : solution to the above system of equations.
More References and links
High School Maths (Grades 10, 11 and 12) - Free Questions and Problems With Answers
Grade 12 Math Practice Test
Middle School Maths (Grades 6, 7, 8, 9) - Free Questions and Problems With Answers
Primary Maths (Grades 4 and 5) with Free Questions and Problems With Answers
Home Page
 .
.


 .
.



 .
.