3D-Vektoren werden zusammen mit Operationen wie Summe, Differenz und skalarer Multiplikation eingeführt. Auch die Eigenschaften wie der Betrag sind enthalten. Fragen mit detaillierten Lösungen sind enthalten.
Ein Vektor ist eine Größe, die sowohl einen Betrag als auch eine Richtung hat. Er wird geometrisch durch ein Liniensegment dargestellt, dessen Länge der Betrag ist, und einen Pfeil, der seine Richtung angibt, wie in der folgenden Abbildung gezeigt. Vektoren werden in der Physik verwendet, um Größen mit Größen und Richtungen wie Geschwindigkeiten, Kräfte, Beschleunigungen zu modellieren; in der Technik, Chemie, Computergrafik, Robotik und vielen anderen Bereichen.
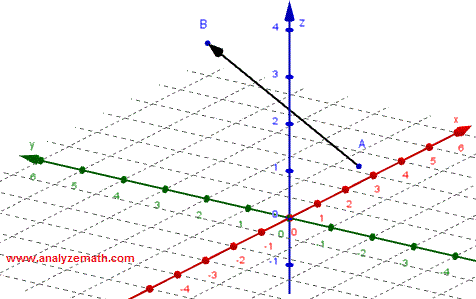
Oben wird der Vektor durch einen Anfangspunkt A und einen Endpunkt B definiert. Daher kann der Vektor als \( \vec{AB} \) bezeichnet werden.
Vektoren mit gleichem Betrag und gleicher Richtung sind äquivalente Vektoren.
Gegeben zwei Vektoren \( \vec{v_1} \) und \( \vec{v_2} \), ist ihre Summe ein Vektor, der erhalten wird, indem zuerst der Vektor \( \vec{v_2} \) so positioniert wird, dass sein Anfangspunkt mit dem Endpunkt von \( \vec{v_1} \) zusammenfällt, und die Summe \( \vec{v_1} + \vec{v_2} \) ist der Vektor, dessen Anfangspunkt der Anfangspunkt von \( \vec{v_1} \) und dessen Endpunkt der Endpunkt von \( \vec{v_2} \) ist. Beachten Sie, dass \( \vec{v_1} + \vec{v_2} = \vec{v_2} + \vec{v_1} \). Außerdem fällt die Summe zweier Vektoren mit der Diagonale des durch \( \vec{v_1} \) und \( \vec{v_2} \) bestimmten Parallelogramms zusammen.
Gegeben zwei Vektoren \( \vec{v_1} \) und \( \vec{v_2} \), kann die Differenz \( \vec{v_2} - \vec{v_1} \) als Summe \( \vec{v_2} + (- \vec{v_1}) \) definiert und geometrisch wie unten gezeigt dargestellt werden.
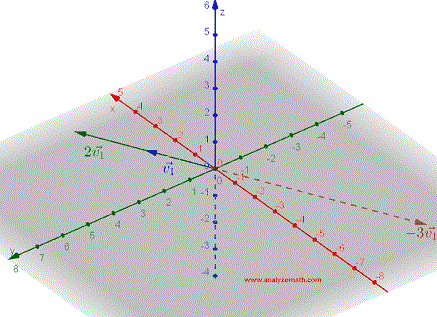
Ein Vektor \( \vec{v_1} \) multipliziert mit einem Skalar \( k \) ist definiert als ein Vektor \( k\vec{v_1} \) parallel zu \( \vec{v_1} \), dessen Richtung dieselbe wie die von \( \vec{v_1} \) ist, wenn \( k \gt 0 \), und entgegengesetzt, wenn \( k \lt 0 \). Der Betrag (die Länge) von \( k\vec{v_1} \) ist \( | k | \) mal der Betrag von \( \vec{v_1} \). Die Abbildung unten zeigt die Vektoren \( \vec{v_1} \), \( 2\vec{v_1} \) und \( -3 \vec{v_1} \).
Ein Einheitsvektor ist ein Vektor mit einem Betrag gleich 1. Unten ist ein 3D-rechtwinkliges Koordinatensystem mit den Einheitsvektoren \(\vec{i} \), \(\vec{j} \) und \(\vec{k} \) in der positiven Richtung der x-, y- bzw. z-Achse dargestellt. Die Vektoren \(\vec{i} \), \(\vec{j} \) und \(\vec{k} \) können durch ihre Komponenten wie folgt definiert werden:
\(\vec{i} = \lt 1 , 0 , 0 >\), eine Einheit entlang der x-Achse.
\(\vec{j} = \lt 0,1,0> \), eine Einheit entlang der y-Achse.
\(\vec{k} = \lt 0 ,0,1> \) , eine Einheit entlang der z-Achse.
Die Komponenten eines beliebigen Vektors \(\vec{v} \) werden definiert, indem \(\vec{v} \) als Summe von Vielfachen der Einheitsvektoren \(\vec{i} \), \(\vec{j} \) und \(\vec{k} \) wie folgt ausgedrückt wird: \[ \vec{v} = 3\vec{i} + 4\vec{j} + 5\vec{k}\] oder in Komponentenform wie folgt: \[ \vec{v} = \lt 3,4,5> \]
Die Komponenten eines Vektors \(\vec{v} \), der durch seinen Anfangspunkt \( A = (x_1 , y_1 ,z_1)\) und seinen Endpunkt \( B = (x_2 , y_2 ,z_2) \) definiert ist, sind gegeben durch \[ \vec{v} = \lt x_2-x_1,y_2-y_1,z_2-z_1> \]
Gegeben sei der Vektor \( \vec{v} = \lt a,b,c> \), sein Betrag (oder seine Länge) ist gegeben durch \[ ||\vec{v}|| = \sqrt{a^2+b^2+c^2} \] Der Einheitsvektor \( \vec{u} \), definiert als ein Vektor mit einem Betrag gleich 1, in der gleichen Richtung wie \( \vec{v} \) ist gegeben durch \[ u = \dfrac{1}{||\vec{v}||} \vec{v} \]
Detaillierte Lösungen und Erklärungen zu den folgenden Fragen sind enthalten.
1) Finden Sie die Komponenten der Vektoren \( \vec{AB} \) und \( \vec{BA}\), wobei A und B Punkte sind, die durch ihre Koordinaten A(2,6,7) und B(0,-3,1) gegeben sind, und zeigen Sie, dass \( \vec{AB} = -1 \vec{BA}\).2) Gegeben sind die Vektoren \(\vec{v_1} = \lt 0,-3,2>\) und \( \vec{v_2} = \lt-3,4,5> \), finden Sie:
3) Gegeben ist der Vektor \(\vec{v} = \lt 0,-3,2>\), finden Sie den Einheitsvektor in der gleichen Richtung wie \(\vec{v} \) und überprüfen Sie, dass sein Betrag gleich 1 ist.
4) Gegeben sind die Punkte A(2,6,7), B(0,-3,1) und C(0,3,4), finden Sie die Komponenten der Vektoren \( \vec{AB} \), \( \vec{AC}\) und \( \vec{BC}\) und zeigen Sie, dass \( \vec{AB} + \vec{BC} = \vec{AC}\).
5) Gegeben sind die Punkte A(-1,2,1), B(2,4,2) und C(5,6,3), finden Sie die Komponenten der Vektoren \( \vec{AB} \), \( \vec{BC}\) und \( \vec{AC}\) und bestimmen Sie, welche dieser Vektoren äquivalent und welche parallel sind.
6) Gegeben sind die Vektoren \(\vec{v_1} = \lt -4,0,2>\) und \( \vec{v_2} = \lt -1,-4,2> \), finden Sie den Vektor \( \vec{v} \), so dass \(\vec{v_1} - 2 \vec{v} = 3 \vec{v} - 3 \vec{v_2} \)
7) Finden Sie einen Vektor in der gleichen Richtung wie der Vektor \( \vec{v} = \lt-4,2,2> \), aber mit der doppelten Länge von \( \vec{v} \).
8) Finden Sie einen Vektor in der entgegengesetzten Richtung des Vektors \( \vec{v} = \lt -1,2,2> \), aber mit einer Länge von 5 Einheiten.
9) Gegeben ist der Vektor \( \vec{v} = \lt -1,2,2> \), finden Sie eine reelle Zahl \( k \) so dass \( ||k \vec{v} || = 1/5 \).
10) Finden Sie \( b \) und \( c \) so, dass die Vektoren \(\vec{v_1} = \lt -4,6,2>\) und \( \vec{v_2} = \lt 2,b,c> \) parallel sind.
11) Sind die drei Punkte A(2,6,7), B(1,4,5) und C(0,2,3) kollinear?
12) Ein Würfel mit einer Seitenlänge von 2 Einheiten ist unten abgebildet.
a) Finden Sie die Komponenten der Vektoren \( \vec{AB} \), \( \vec{EF} \), \( \vec{DC} \), \( \vec{HG} \), \( \vec{AC} \) und \( \vec{AG} \).
b) Welche der Vektoren in Teil a) sind äquivalent?
c) Beweisen Sie algebraisch, dass \( \vec{AB} + \vec{BF} + \vec{FG} = \vec{AC} + \vec{CG} \).
d) Finden Sie \( || \vec{AG} || \).
e) Finden Sie den Einheitsvektor in der gleichen Richtung wie der Vektor \( \vec{AG} \).
Detaillierte Lösungen und Erklärungen zu diesen Fragen.