Complex Numbers in Exponential Form

Complex numbers are written in exponential form . The multiplications, divisions and power of complex numbers in exponential form are explained through examples and reinforced through questions with detailed solutions.

Exponential Form of Complex Numbers

A complex number in standard form \( z = a + ib \) is written in polar form as \[ z = r (\cos(\theta)+ i \sin(\theta)) \] where \( r = \sqrt{a^2+b^2} \) is called the modulus of \( z \) and \( \tan (\theta) = \left (\dfrac{b}{a} \right) \) , such that \( 0 \le \theta \lt 2\pi \) , \( \theta\) is called argument Examples and questions with solutions. of \( z \)
The graphical interpretations of \( a \) , \( b \) , \( r \) and \( \theta \) are shown below for a complex number on a complex plane.

complex plane


We now use Euler's formula given by \( \displaystyle e^{i\theta} = \cos \theta + i \sin \theta \) to write the complex number \( z \) in exponential form as follows: \[ z = r e^{i\theta}\] where \( r \) and \( \theta \) as defined above.

Example 1
Plot the complex number \( z = -1 + i \) on the complex plane and write it in exponential form .
Solution to Example 1
The complex number \(z = -1 + i = a + i b \) with \( a = -1 \) being the real part and \( b = 1 \) being the imaginary part, is plotted as a vector on a complex plane shown below. It is a vector whose components are the real part \( a \) along the "real axis" and the imaginary part \( b \) along the "imaginary axis". The argument angle \( \theta \) is the angle in counterclockwise direction with initial side starting from the positive real part axis. The modulus \( r = \sqrt {a^2+b^2} = \sqrt {(-1)^2+(1)^2} = \sqrt 2\) is the length of the vector.

plot of complex number z = -1 + i on complex plane


\(z = -1 + i = a + i b\)
gives \( a = - 1 \) and \( b = 1 \)
\( r = \sqrt {a^2 + b^2} = \sqrt {(-1)^2 + 1^2} = \sqrt {1 + 1} = \sqrt 2\)
We first need to find the reference angle \( \theta_r \) which is the acute angle between the terminal side of \( \theta \) and the real part axis.
\( \theta_r = \tan^{-1}\left|\dfrac{b}{a}\right| = \tan^{-1}\left|\dfrac{1}{-1}\right| =\tan^{-1} (1) = \dfrac{\pi}{4}\)
The real part of \(z\) is negative and its imaginary part is posiive, hence the terminal side of \( \theta \) is in quadrant II (see plot of \( z \) above).
\( \theta \) is computed as follows:
\( \theta = \pi - \theta_r = \pi - \dfrac{\pi}{4} = \dfrac{3\pi}{4}\)
\( z \) in exponential form is given by
\( z = \sqrt2 e^{i\dfrac{3\pi}{4}} \)

Example 2
a) Plot the complex numbers : \( i , - 2 , - i , - 1 - 2i \) and \( 1 - i \) on the same complex plane.
b) Plot in separate complex planes and write the complex numbers : \( i , - 2 , - i , - 1 - 2i \) and \( 1 - i \) in exponential form .

Solution to Example 2
a) The plot all given complex numbers in the same complex plane is shown below.

plot of complex numbers in example 2 on complex plane



b) Plot and write in exponential forms .
Let \( z = i = a + i b \)
gives \( a = 0 \) and \( b = 1 \)
\( r = \sqrt {0^2 + 1^2} = 1 \)
\( \tan \theta = \dfrac{1}{0} = undefined \)
An angle whose tangent is undefined is an angle with terminal side on the imaginary axis.
In fact it is easier to determine \( \theta = \dfrac{\pi}{2} \) from the plot of \( z = i \) shown below.
Write in exponential form : \( \quad z = i = r e^{i\theta} = e^{i\pi/2} \)

plot of complex number i



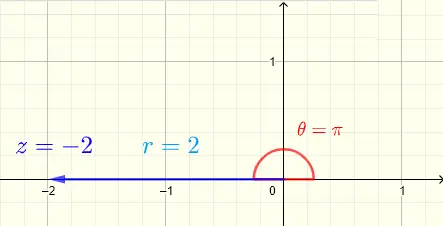
Let \( z = -2 = a + i b \)
gives \( a = -2 \) and \( b = 0 \)
\( r = \sqrt {(-2)^2 + 0^2} = 2 \)
\( \tan \theta = \dfrac{0}{-2} = 0 \)
An angle whose tangent is equal to 0 is an angle with terminal side on the real axis.
It is easier to determine \( \theta = \pi \) from the plot of \( z = -2 \) shown below.
Write in exponential form : \( \quad z = -2 = r e^{i\theta} = 2 e^{i\pi} \)

plot of complex number -2



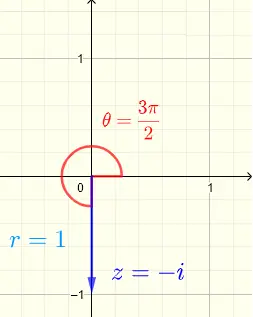
Let \( z = - i = a + i b \)
gives \( a = 0 \) and \( b = - 1 \)
\( r = \sqrt {0^2 + (-1)^2} = 1 \)
\( \tan \theta = \dfrac{-1}{0} = undefined \)
An angle whose tangent is undefined is an angle with terminal side on the imaginary axis.
We determine \( \theta = \dfrac{3\pi}{2} \) from the plot of \( z = - i \) shown below.
Write in exponential form : \( \quad z = - i = r e^{i\theta} = e^{ i 3\pi/2} \)

plot of complex number -i



Let \( z = - 1 -2i = a + i b \)
gives \( a = -1 \) and \( b = - 2 \)
\( r = \sqrt {(-1)^2 + (-2)^2} = \sqrt 5 \)
First find reference angle: \( \tan \theta_r = |\dfrac{-2}{-1}| = 2 \) , \( \theta_r = \arctan 2 \)
\( \theta = \pi + \arctan 2 \approx 4.25\)
Write in exponential form : \( \quad z = - 1 -2i = r e^{i\theta} = \sqrt 5 e^{i (\pi + \arctan 2)} \)

plot of complex number -1-2i



Let \( z = 1 - i = a + i b \)
gives \( a = 1 \) and \( b = - 1 \)
\( r = \sqrt {(1)^2 + (-1)^2} = \sqrt 2 \)
First find reference angle: \( \tan \theta_r = |\dfrac{-1}{1}| = 1 \) , \( \theta_r = \dfrac{\pi}{4} \)
\( \theta = 2\pi - \theta_r = 2\pi - \dfrac{\pi}{4} = \dfrac{7\pi}{4} \)
Write in exponential form : \( \quad z = 1 - i = r e^{i\theta} = \sqrt 2 e^{i ( 7 \pi/4)} \)

plot of complex number 1 - i




Example 3
Write complex number \( z = \sqrt2 e^{ i \dfrac{5\pi}{4}} \) in standard form.
Solution to Example 3
\( z = \sqrt2 e^{ i \dfrac{5\pi}{4}} \)
Use Euler's formula
\( = \sqrt2(\cos(\dfrac{5\pi}{4})+ i \sin(\dfrac{5\pi}{4})) \)
Simplify
\( = \sqrt2(-\dfrac{\sqrt2}{2} - i \dfrac{\sqrt2}{2}) \)
\( = - 1 - i \)

Complex numbers in exponential form are easily multiplied and divided. The power and root of complex numbers in exponential form are also easily computed

Multiplication of Complex Numbers in Exponential Forms

Let \( z_1 = r_1 e^{ i \theta_1} \) and \( z_2 = r_2 e^{ i \theta_2} \) be complex numbers in exponential form .
The product of \( z_1 \) and \( z_2 \) is given by
\[ z_1 z_2 = r_1 r_2 e ^{ i (\theta_1+\theta_2) } \]

Example 3
Given \( z_1 = 3 e^{ i \pi/4 } \) and \( z_2 = 5 e^{i 3\pi/4 } \)
Find \( z_1 z_2\) and write it in standard form.
Solution to Example 3
\( z_1 z_2 = (3 e^{ i \pi/4 }) (5 e^{ i 3 \pi/4 } )\)
Multiply the modulii \( 3 \) and \( 5 \) together and apply exponent rule apply the rule of exponents \( e^x e^y = e^{x+y} \)
\( = (3 \times 5) e^{ i\pi/4 + i 3\pi/4 } \)
Simplify
\( = 15 e^{ i \pi } \)
Rewrite in polar form
\( = 15 (\cos \pi + i \sin \pi) \)
Simplify
\( = - 15 \)



Division of Complex Numbers in Exponential Forms

Let \( z_1 = r_1 e^{ i \theta_1} \) and \( z_2 = r_2 e^{ i \theta_2 } \) be complex numbers in exponential form .
The ratio (or division) of \( z_1 \) and \( z_2 \) is given by
\[ \dfrac{z_1}{ z_2} = \dfrac{r_1}{r_2} e ^{ i (\theta_1-\theta_2) } \]

Example 4
Given \( z_1 = 10 e^{ i \pi/3 } \) and \( z_2 = 2 e^{ i 2\pi/3 } \)
Find the product \( \dfrac{z_1}{z_2} \) and write it in standard form.
Solution to Example 4
\( \dfrac{z_1}{z_2} = \dfrac{10 e^{ i \pi/3 }} {2 e^{ i 2 \pi/3 } }\)
Divide the modulii \( 10 \) by \( 2 \) and apply the rule of exponents \( \dfrac{e^x}{e^y} = e^{x-y} \)
\( = \dfrac {10}{2} e^{ i ( \pi/3 - 2\pi/3 ) } \)
\( = 5 e^{ - i \pi/3 } \)
Rewrite in polar form
\( = 5 (\cos (- \pi/3) + i \sin (- \pi/3) ) \)
Simplify
\( = 5(1/2 - \dfrac{\sqrt 3}{2} i) = \dfrac{5}{2} - \dfrac{5\sqrt3}{2} i \)


You may also review De Moivre's Theorem Power and Root of Complex Numbers .

Questions

1) Write the following complex numbers in exponential forms .
  1. \( z_1 = - 1 \)
  2. \( z_2 = - 2 i \)
  3. \( z_3 = -\sqrt3 - i \)
  4. \( z_4 = - 3 + 3\sqrt 3 i \)
  5. \( z_5 = 7 - 7 i \)
.

2) Use the results in part a) above to evaluate the following expressions and write them in exponential form .
  1. \( z_4 z_5 \)
  2. \( \dfrac{z_3 z_5}{z_4} \)
.

Solutions to the Above Questions

1)
  1. \( z_1 = -1 = e^{ i \pi} \)
  2. \( z_2 = - 2 i = 2 e^{ i 3\pi/2 } \)
  3. \( z_3 = -\sqrt3 - i = 2 e^{ i 7\pi/6}\)
  4. \( z_4 = - 3 + 3\sqrt 3 i = 6 e^{ i 2\pi/3 } \)
  5. \( z_5 = 7 - 7 i = 7 \sqrt 2 e^{ i 7\pi/4} \)
.

2)
  1. \( z_4 z_5 = (6 e^{ i 2\pi/3 }) (7 \sqrt 2 e^{ i 7\pi/4}) \)
    Use rule of multiplication given above
    \( = 42 \sqrt 2 e^{i(2\pi/3 + 7\pi/4)} \)
    Simplify
    \( = 42 \sqrt 2 e^{i 29\pi/12} \)
    Argument is larger than \( 2 \pi \) therefore you may subtract \( 2 \pi \) from it
    \( = 42 \sqrt 2 e^{i (29\pi/12-2\pi )} \)
    Simplify
    \( = 42 \sqrt 2 e^{i 5\pi/12 } \)

  2. \( \dfrac{z_3 z_5}{z_4} = \dfrac{( 2 e^{ i 7\pi/6})(7 \sqrt 2 e^{ i 7\pi/4})}{6 e^{ i 2\pi/3 }} \)
    Use rule of multiplication and division given above
    \( = \dfrac{2 \times 7 \sqrt 2}{6} e^{i(7\pi/6 + 7\pi/4 - 2\pi/3)} \)
    Simplify
    \( = \dfrac{7\sqrt{2}}{3} e^{i 9\pi/4} \)
    Argument is larger than \( 2 \pi \) therefore you may subtract \( 2 \pi \) from it
    \( = \dfrac{7\sqrt{2}}{3} e^{i (9\pi/4- 2\pi) } \)
    Simplify
    \( \dfrac{7\sqrt{2}}{3} e^{i \pi/4 } \)
.

More References and Links

Modulus and Argument of Complex Numbers Examples and questions with solutions.
Convert a Complex Number to Polar and Exponential Forms Calculator
Complex Numbers in Polar Form
Euler's formula .
Complex Numbers - Basic Operations
Find the Reference Angle
Sum and Difference Formulas in Trigonometry
Convert a Complex Number to Polar and Exponential Forms - Calculator
Algebra and Trigonometry - R. E. LARSON, R. P. Hostetler, B. H. Edwards, D.E Heyd,
Houghton Mifflin Company - ISBN: 0-669-41723-8
{ezoic-ad-1}
{ez_footer_ads}