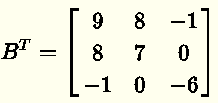方形 矩阵 A 是对称的当且仅当 A = AT 其中 AT 是矩阵 的转置 一个。
对称矩阵可以通过视觉识别：相对于主对角线对称放置的条目是相等的，如下面的对称矩阵示例所示。
这些是对称矩阵的示例。
a)
通过简单的检查，相对于主对角线对称放置的条目都等于 -2 ，因此矩阵 A 是对称的。
另外，矩阵 A 的转置是通过将矩阵的行交换为列来获得的。 矩阵的转置
A is
请注意， AT = A ，因此矩阵 A 是对称的。
b)
矩阵 B 的转置是通过将矩阵的列交换为行来获得的。 矩阵 B 的转置为
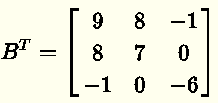
请注意， BT = B ，因此矩阵 B 是对称的。
对于任何大小为 \( m \times n\) 的矩阵 \( A \) ，矩阵 \( A A^T \) 和 \( A^T A \) 是对称的，并且大小为 \( m \times m \) 和 \( n \times n \) 分别。
让 \(
A =
\begin{bmatrix}
-3 & -3 & 9\\
2 & -7 & 1
\end{bmatrix}
\) 是一个 \( 2 \times 3 \) 矩阵
\( A^T =
\begin{bmatrix}
-3 & 2\\
-3 & -7 \\
9 & 1
\end{bmatrix}
\)
\( A A^T = \begin{bmatrix}
-3 & -3 & 9\\
2 & -7 & 1
\end{bmatrix}
\begin{bmatrix}
-3 & 2\\
-3 & -7 \\
9 & 1
\end{bmatrix} \)
\( \quad \quad = \begin{bmatrix}
99 & 24\\
24 & 54
\end{bmatrix}
\)
因此 \( A A^T \) 是一个 \( 2 \times 2 \) 对称矩阵。
\( A^T A =
\begin{bmatrix}
-3 & 2\\
-3 & -7 \\
9 & 1
\end{bmatrix}
\begin{bmatrix}
-3 & -3 & 9\\
2 & -7 & 1
\end{bmatrix}
\)
\( \quad \quad =
\begin{bmatrix}
13 & -5 & -25\\
-5 & 58 & -34\\
-25 & -34 & 82
\end{bmatrix}
\) is a \( 3 \times 3 \)
因此 \( A^T A \) 是一个 \( 3 \times 3 \) 对称矩阵。
下面给出了对称矩阵的一些最重要的属性。
例子 1
下列矩阵中哪一个是对称矩阵？
a) \( A =
\begin{bmatrix}
0 & -1 & 1 \\
-1 & 0 & 0
\end{bmatrix} \) b) \( B =
\begin{bmatrix}
-2 & 0 & 1 \\
0 & 0 & 1 \\
1 & 1 & 1
\end{bmatrix} \) c) \( C =
\begin{bmatrix}
5 & -7 & 0 & 0\\
5 & -7 & 0 & 0\\
5 & -7 & 0 & 0\\
5 & -7 & 0 & 0
\end{bmatrix} \)
d) \( D =
\begin{bmatrix}
1 & 4 & 0 & 9\\
4 & 2 & -4 & 0\\
0 & -4 & 4 & 0\\
9 & 0 & 0 & -5
\end{bmatrix} \)
解决办法
矩阵 \( B \) 和 \( D \) 是对称的。
例子 2
对称矩阵 \( A \) 和 \( B \) 由下式给出 \( A =
\begin{bmatrix}
-1 & 1 \\
1 & 2
\end{bmatrix} \) , \( B =
\begin{bmatrix}
4 & 2 \\
2 & -3
\end{bmatrix} \).
证明 \( A+B \) 和 \( A-B \) 是对称的。 （验证属性2）
解决办法
计算 \( A + B \)
\( A + B =
\begin{bmatrix}
-1 & 1 \\
1 & 2
\end{bmatrix} + \begin{bmatrix}
4 & 2 \\
2 & -3
\end{bmatrix} \)
\( \quad =
\begin{bmatrix}
3 & 3 \\
3 & -1
\end{bmatrix}
\)
计算 \( A - B \)
\( A - B =
\begin{bmatrix}
-1 & 1 \\
1 & 2
\end{bmatrix} - \begin{bmatrix}
4 & 2 \\
2 & -3
\end{bmatrix}
\)
\( \quad =
\begin{bmatrix}
-5 & -1 \\
-1 & 5
\end{bmatrix}
\)
因此 \( A + B \) 和 \( A - B \) 也是对称矩阵。
例子 3
求对称矩阵的 的逆 \( A =
\begin{bmatrix}
-1 & -2\\
-2 & 0
\end{bmatrix} \)
并证明该逆矩阵也是对称的。（验证性质4）
解决办法
使用 \( 2 \times 2 \) 矩阵的逆矩阵的公式 \( \begin{bmatrix}
x & y \\
z & w \\
\end{bmatrix}^{-1} = \dfrac{1}{xw - yz}
\begin{bmatrix}
w & - y \\
- z & x \\
\end{bmatrix} \) to find \( A^{-1} \)
\( A^{-1} = \dfrac{1}{-4}
\begin{bmatrix}
0 & 2\\
2 & -1
\end{bmatrix}
\)
\( \quad \quad =
\begin{bmatrix}
0 & -\dfrac{1}{2}\\
-\dfrac{1}{2} & \dfrac{1}{4}
\end{bmatrix}
\)
因此 \( A^{-1} \) 也是对称的.
例子 4
设矩阵 \( A =
\begin{bmatrix}
-3 & 1\\
1 & 7
\end{bmatrix} \)
计算 \( A^3 \) 并验证它是对称的。 （验证属性6）
解决办法
\( A^3
=
\begin{bmatrix}
-3 & 1\\
1 & 7
\end{bmatrix}
\begin{bmatrix}
-3 & 1\\
1 & 7
\end{bmatrix}
\begin{bmatrix}
-3 & 1\\
1 & 7
\end{bmatrix}
\)
\( \quad \quad =
\begin{bmatrix}
10 & 4\\
4 & 50
\end{bmatrix}
\begin{bmatrix}
-3 & 1\\
1 & 7
\end{bmatrix}
\)
\( \quad \quad =
\begin{bmatrix}
-26 & 38\\
38 & 354
\end{bmatrix}
\)
因此 \( A^3 \) 是一个对称矩阵。
例子 5
找到实数 \(a \)、\( b \) 和 \( c \) 使得矩阵 \( A =
\begin{bmatrix}
0 & a+b & c+2 \\
a & 2 & c \\
4 & a+b & 4
\end{bmatrix} \)
是对称的。
解决办法
为了使给定的矩阵是对称的，我们必须同时满足以下方程：
\( a = a + b \) ,
\( c + 2 = 4 \) ,
\( c = a + b \)
求解上面\(a,\;b,\;c\)中的方程组，得到
\( b = 0 , \; c = 2 , \; a = 2 \) 是使给定矩阵对称的值。
例子 6
给定对称矩阵 \( A =
\begin{bmatrix}
-1 & 3 \\
3 & 4
\end{bmatrix} \) 和 \( B =
\begin{bmatrix}
4 & 8 \\
8 & 9
\end{bmatrix} \), 验证 \( AB + BA \) 也是对称的（上面的性质 3）
解决办法
计算 \( AB \)
\( AB = \begin{bmatrix}
-1 & 3 \\
3 & 4
\end{bmatrix} \begin{bmatrix}
4 & 8 \\
8 & 9
\end{bmatrix}
\)
\( \quad \quad =
\begin{bmatrix}
20 & 19 \\
44 & 60
\end{bmatrix} \)
计算 \( BA \)
\( BA = \begin{bmatrix}
4 & 8 \\
8 & 9
\end{bmatrix} \begin{bmatrix}
-1 & 3 \\
3 & 4
\end{bmatrix}
\)
\( \quad \quad =
\begin{bmatrix}
20 & 44\\
19 & 60
\end{bmatrix} \)
计算 \( AB + BA \)
\( AB + BA = \begin{bmatrix}
20 & 19 \\
44 & 60
\end{bmatrix}
+
\begin{bmatrix}
20 & 44\\
19 & 60
\end{bmatrix}
\)
\( \quad \quad =
\begin{bmatrix}
40 & 63\\
63 & 120
\end{bmatrix} \)
因此 \( AB + BA \) 是一个对称矩阵。