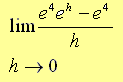 =
=
解决方案
当 h → 0
lim (e4 eh - e4) / h = (e4 e0 - e4) / 0
= 0 / 0 , 极限中的不确定形式
需要另一种方法。 令 f(x) = ex。 给定的极限可以写成如下: x → H
lim (e4 eh - e4) / h = lim (e4 + h - e4) / h = limit [ f(4+h) - f(4) ] / h
这是 f(x) = ex 在 x = 4 处的一阶导数的定义。因此为 x → h
lim (e4 eh - e4) / h = e 4
函数 g 的图形由下式定义

将有垂直渐近线
解决方案
如果可能的话,让我们首先简化给定的有理函数
g(x) = (x3 + 2x2 - 3x) / (x2 + 2x - 3)
= x (x2 + 2x - 3) / (x2 + 2x - 3) = x
函数 g 无垂直渐近线
鉴于

查找

解决方案
使用该定理,该定理表明总和的极限等于极限的总和。 因此作为 x → 0,
lim (x + 4x2 + sin x) / 3x = lim (x / 3x) + lim (4x2 / 3x) + (1/3) sin x / x
简化
= lim (1/3) + lim (4x) + (1/3) sin x / x
= 1/3 + 0 + (1/3)*1 = 2/3
函数 f 定义为
 。
。 求 df(x) / dx。
解决方案
使用指出函数和的导数是导数之和的定理,我们可以写
d/dx [ 2x3sin(x) + (1/x)tan(x) + x sec(x) + 2 ]
= d/dx [ 2x3sin(x) ] + d/dx [ (1/x)tan(x) ] + d/dx [ x sec(x) ] + d/dx [ 2 ]
我们现在计算上面每一项的导数
d/dx [ 2x3sin(x) ] = 2 [ 3x2 sin(x) + x3 cos(x) ] = 6x2 sin(x) + 2x3 cos(x)
d/dx [ (1/x)tan(x) ] = - (1/x2) tan(x) + (1/x) sec2(x))
d/dx [ x sec(x) ] = sec(x) + x sin(x) sec2(x)
d/dx [ 2 ] = 0
因此
df/dx = 6x2 sin(x) + 2x3 cos(x) - (1/x2)tan(x) + (1/x sec2(x)) + sec(x) + x sin(x) sec2(x)
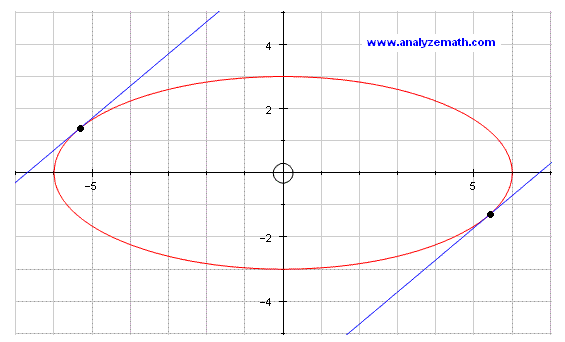
曲线 C 由方程 0.25 x2 + y2 = 9 描述。确定曲线 C 上切线斜率为 1 的点的 y 坐标。
解决方案
让我们计算一阶导数。 对给定方程两边求微分
0.25 (2x) + 2 y y ' = 0
y ' = - 0.5 x / (2 y)
现在,我们求解给定方程 0.25 x2 + y2 = 9(对于 x)
x = ± sqrt [ (9 - y2) / 0.25 ]
将 x 代入 y ' = - 0.5 x / (2 y) 带有 ± sqrt [ (9 - y2) / 0.25 ]
y ' = - 0.5 (± sqrt [ (9 - y2) / 0.25 ] / (2 y)
切线的斜率为 1。因此
- 0.5 (±sqrt [ (9 - y2) / 0.25 ] )/ (2 y) = 1
对 y 求解上述问题。 两种解决方案
y = 3 sqrt(5) / 5
y = - 3 sqrt(5) / 5
下面显示了 0.25 x2 + y2 = 9 的图形以及两条切线。
求微分方程 dy/dx = cos(x) / y2 的解,其中 y(π/2) = 0。
解决方案
微分方程中的变量可以分离如下
y2 dy = cos(x) dx
将双方整合起来
∫ y2 dy = ∫ cos(x) dx
(1/3) y3 = sin(x) + C , 其中 C 是积分常数
现在我们使用条件 y(π/2) = 0 来求常数 C
(1/3) y3(π/2) = sin(π/2) + C
0 = 1 + C
C = - 1
将 (1/3) y3 = sin(x) + C 中的 C 代入 -1 并求解 y
(1/3) y3 = sin(x) - 1
y3 = 3(sin(x) - 1)
y = (3 sin(x) - 3)1/3
解决方案
设 u = cos x,因此 du/dx = - sin x。 现在,我们在给定积分中用 u 代替 cos x,用 - du/dx 代替 sin x。 因此
∫ cos4(x)sin(x) dx = ∫ u4 (-du/dx) dx
= - ∫ u4du
= (-1/5)u5 + C , 其中 C 是积分常数
= (-1/5)cos5(x) + C
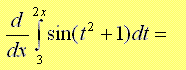
解决方案
令 u = 2x,因此 du/dx = 2 或 dx = du / 2。因此给定积分变为
d/dx ∫ 32xsin(t2 + 1) dt = 2 d/du ∫ 3usin(t2 + 1) dt
利用微积分基本定理,我们得到
= 2 sin(u2 + 1)
将 u 替换为 2x
= 2 sin(4x2 + 1)
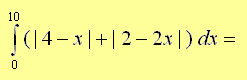
解决方案
我们首先分析表达式 4 - x 和 2 - 2x 在积分极限 0 和 10 之间的符号。4 - x 在 x = 4 处改变符号,2 - 2x 在 x = 1 处改变符号。
对于 0 到 4 之间的 x:4 - x 为正,因此 |4 - x| = 4 - x
对于 4 到 10 之间的 x:4 - x 为负数,因此 |4 - x| = -(4 - x)
对于介于 0 和 1 之间的 x:2 - 2x 为正,因此 |2 - 2x| = 2 - 2x
对于 1 到 10 之间的 x:2 - 2x 是负数,因此 |2 - 2x| = -(2 - 2x)
现在,我们将给定积分重写为两个积分之和,如下所示。
∫ 010 (|4 - x|+|2 - 2x|) dx =
∫ 010 (|4 - x|) dx + ∫ 010 (|2 - 2x|) dx
现在我们按如下方式计算上述每个单独的积分。
∫ 010 (|4 - x|) dx = ∫ 04 (4 - x) dx + ∫ 410 -(4 - x) dx = 8 + 18 = 26
and
∫ 010 (|2 - 2x|) dx = ∫ 01 (2 - 2x) dx + ∫ 110 -(2 - 2x) dx = 1 + 81 = 82
我们现在有
∫ 010 (|4 - x|) dx + ∫ 010 (|2 - 2x|) dx = 26 + 82 = 108
评估

解决方案
设 u = 5 + x3/4 ,因此 du/dx = (3/4) 1/x1/4 并代入给定积分
∫ (5 + x3/4)9 / (x1/4) dx = ∫ [ ( u9 ) / (x1/4) ] (4/3) x1/4 du
= (4/3) ∫ u9 du
= (4/3) (1/10) u10
= (2/15) (5 + x3/4)10
鉴于函数 h 定义为
求h'(x).
解决方案
设 u = arctan(x3 + 1) + 2x。 因此函数 h 可以写为
h(x) = u4 h '(x) = 4 u3 u'
现在我们让 v = arctan(x3 + 1) 并计算 u '
u ' = (v ')( 1 / (1 + v2) )
= (3x2) / (1 + (x3 + 1)2)
= (3x2) / (x6 + 2x3 + 2)
因此
h '(x) = 4 (arctan(x3 + 1) + 2x)3 (3x2) / (x6 + 2x3 + 2)
函数h的图形如下所示。 h 的一阶导数 h' 有多少个零?
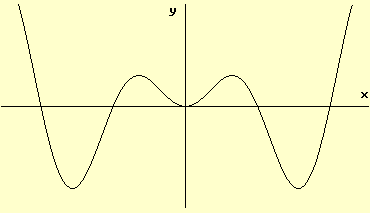
解决方案
每当 h 的图具有局部最大值或局部最小值时,h '(x) 就等于 0。给定图具有 3 个局部最小值和 2 个局部最大值,因此 h ' 有 5 个零。
多项式 f 的图形如下所示。 如果 f' 是 f 的一阶导数,则 f'(x) 除以 x - b 的余数更有可能等于

解决方案
f 的图形在 b 处有局部最大值,因此 f'(b) = 0。由于 f 是多项式,因此 f ' 也是多项式函数,使得 f '(b) = 0 并且根据余数定理,除法 f '(x) 除以 x - b 等于 o。
所有点的集合 (ln(t - 2) , 3t),其中 t 是大于 2 的实数,是具有方程的曲线图
解决方案
给定的参数方程可以写为
x(t) = ln(t - 2) and y(t) = 3t
求解 y(t) = 3t 得到 t 以获得
t = y / 3
将 x(t) = ln(t - 2) 中的 t 替换为 y / 3
x = ln(y / 3 - 2)
求解 y
y/3 - 2 = ex
对y求解上述方程,得到曲线方程
y = 3 ( ex + 2 )
设 P(x) = 2 x3 + K x + 1。如果 P(x) 除以 x - 2 的余数等于 10,则求 K。
解决方案
余数定理指出 P(x) 除以 x - 2 等于 P(2)。 因此
P(2) = 2 (2)3 + K (2) + 1 = 10
求解 K
K = - 7/2
函数 f 的定义如下
 .
.
其中 C 是常数。 为了使函数 f 在 x = 0 处连续,C 的值必须等于多少?
解决方案
为了使函数 f 在 x = 0 处连续,当 x 接近时 lim f(x) 必须等于 f(0)。 我们首先找到当 x 接近 0 时 f(x) 的极限。 作为 x → 0,
lim [ sqrt(4x + 4) - sqrt(2x + 4) ] / 2x = 0 / 0 , 不确定形式的极限
需要另一种方法。 将分子和分母乘以 sqrt(4x + 4) - sqrt(2x + 4),化简并找到极限。 作为 x ∫ 0,
lim [ sqrt(4x + 4) - sqrt(2x + 4) ] / 2x
= lim [ sqrt(4x + 4) - sqrt(2x + 4) ] [ sqrt(4x + 4) + sqrt(2x + 4) ]/ [ 2x [ sqrt(4x + 4) + sqrt(2x + 4) ] ]
= lim [4x + 4 - 2x - 4] / [ 2x [ sqrt(4x + 4) + sqrt(2x + 4) ] ]
= lim 2x / [ 2x [ sqrt(4x + 4) + sqrt(2x + 4) ] ]
= lim 1 / [ sqrt(4x + 4) + sqrt(2x + 4) ]
= 1 / [ 2 + 2 ] = 1/4
为了使 f 连续,我们需要有
C = 1/4
f 和 g 是满足 f '(x) = g(x) 和 g '(x) = f(x) 的函数。 (f . g)(x) 的二阶导数等于
A) f "(x) g "(x)
B) g '(x) g(x) + f(x) f '(x)
C) 4 g(x) f(x)
D) 2 g(x) f(x)
E) g(x) f(x)
解决方案
的一阶导数 (f . g)(x)
(f . g) ' = f ' g + f g '
的二阶导数 (f . g)(x)
(f . g) " = (f ' g + f g ') '
= f "g + f 'g' + f 'g' + f g" (I)
请注意,由于 f '(x) = g(x) 且 g '(x) = f(x),我们有
f " = g' and g " = f'
将 f " 和 g " 代入上式(I)中可得
(f . g) " = g 'g + f 'g' + f 'g' + f f'
现在,我们将 g ' 替换为 f,将 f ' 替换为 g 以获得
(f . g) " = fg + gf+ fg + f g = 4 fg
由 f(x) = sin(x) + x 定义的函数 f 在闭区间 [0 , π] 上的平均变化率等于
解决方案
函数从 a 到 b 的平均变化率定义为
(f(b) - f(a)) / (b - a)
将上面的定义应用到上面的问题上
(f(π) - f(0)) / (π - 0) = [ (sin(π) + π) - (sin(0)+ 0) ] / (π - 0) = 1
该图显示了半个周期内 y = sin(x) 的图形以及 y = 1/2 线。 求阴影区域的面积。
 .
.
解决方案
直线 y = 1/2 和 f 的图形的交点的 x 坐标可通过求解找到
sin(x) = 1/2 , for 0 ≤ x ≤ π
解决办法: x = π / 6 and x = 5π / 6
我们首先将要计算的面积分成3部分,如下所示.
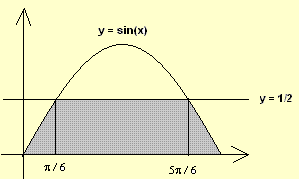 .
.
计算三部分相加的面积 A(注意中间的面积是矩形的面积):
A = ∫0π/3 sin(x) dx+ 1/2(5Pi/6 - Pi/6) + ∫5π/6π sin(x) dx
= [ - cos(x) ]0π/3 + π / 3 + [- cos(x)]5π/6π
= 2 + π / 3 - sqrt(3)
函数 f、g 和 h 定义如下:g(x) = f(x2)、f(x) = h(x3 + 1) 和 h '(x) = 2x + 1
求 g'(x).
解决方案
让我们用 h 来表达 g(x)
sin(x) = 1/2 , for 0 ≤ x ≤ π
g(x) = f(x2) = h( (x2)3 + 1 )
= h(x6 + 1)
设 u = x6 + 1。因此
g(x) = h(u) , 和 u = x6 + 1
利用微分链式法则写出
g '(x) = (du/dx) (dh/du)
如果 h'(x) = 2x + 1,则
dh/du = h '(u) = 2u + 1
因此
g '(x) = 6x5 [ 2u + 1 ]
将 u 替换为 g '(x) 中的 x6 + 1
g '(x) = 6x5 [ 2(x6 + 1) + 1 ] =
= 12 x11 + 18 x5