Graphs and Properties of Trigonometric Functions

This page presents the main properties of the six trigonometric functions: \( \sin x \), \( \cos x \), \( \tan x \), \( \cot x \), \( \sec x \), and \( \csc x \). For each function, we discuss the graph, domain, range, period, symmetry, intercepts, extrema, monotonic intervals, and asymptotes (when applicable).

Sine Function: \( f(x) = \sin x \)

• Domain: all real numbers
• Range: \([-1, 1]\)
• Period: \(2\pi\)
• x-intercepts: \(x = k\pi,\; k \in \mathbb{Z}\)
• y-intercept: \(y = 0\)
• Maximum points: \(\left(\frac{\pi}{2} + 2k\pi,\, 1\right)\)
• Minimum points: \(\left(\frac{3\pi}{2} + 2k\pi,\,-1\right)\)
• Symmetry: Since \( \sin(-x) = -\sin x \), the sine function is odd and symmetric about the origin.
• Increasing/Decreasing: Over one period \([0, 2\pi]\), \( \sin x \) increases on \( (0, \frac{\pi}{2}) \cup (\frac{3\pi}{2}, 2\pi) \) and decreases on \( (\frac{\pi}{2}, \frac{3\pi}{2}) \).

Cosine Function: \( f(x) = \cos x \)

• Domain: all real numbers
• Range: \([-1, 1]\)
• Period: \(2\pi\)
• x-intercepts: \(x = \frac{\pi}{2} + k\pi\)
• y-intercept: \(y = 1\)
• Maximum points: \((2k\pi, 1)\)
• Minimum points: \((\pi + 2k\pi, -1)\)
• Symmetry: Since \( \cos(-x) = \cos x \), the cosine function is even and symmetric about the y-axis.
• Increasing/Decreasing: Over \([0, 2\pi]\), \( \cos x \) decreases on \((0, \pi)\) and increases on \((\pi, 2\pi)\).

Tangent Function: \( f(x) = \tan x \)

• Domain: all real numbers except \( x = \frac{\pi}{2} + k\pi \)
• Range: all real numbers
• Period: \( \pi \)
• x-intercepts: \( x = k\pi \)
• y-intercept: \( y = 0 \)
• Symmetry: Since \( \tan(-x) = -\tan x \), tangent is an odd function.
• Increasing: \( \tan x \) is increasing on each interval \( \left(-\frac{\pi}{2} + k\pi,\, \frac{\pi}{2} + k\pi\right) \).
• Vertical asymptotes: \( x = \frac{\pi}{2} + k\pi \)

Cotangent Function: \( f(x) = \cot x \)

• Domain: all real numbers except \( x = k\pi \)
• Range: all real numbers
• Period: \( \pi \)
• x-intercepts: \( x = \frac{\pi}{2} + k\pi \)
• Symmetry: Since \( \cot(-x) = -\cot x \), cotangent is an odd function.
• Decreasing: Over one period \((0, \pi)\), \( \cot x \) is decreasing.
• Vertical asymptotes: \( x = k\pi \)

Secant Function: \( f(x) = \sec x \)

• Domain: all real numbers except \( x = \frac{\pi}{2} + k\pi \)
• Range: \( (-\infty, -1] \cup [1, \infty) \)
• Period: \( 2\pi \)
• y-intercept: \( y = 1 \)
• Symmetry: Since \( \sec(-x) = \sec x \), secant is an even function.
• Vertical asymptotes: \( x = \frac{\pi}{2} + k\pi \)

Cosecant Function: \( f(x) = \csc x \)

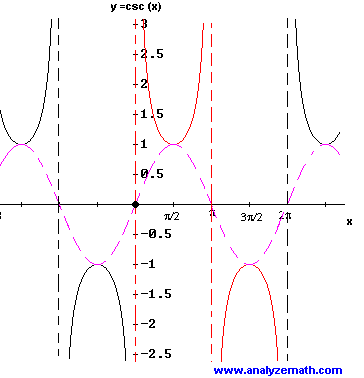
• Domain: all real numbers except \( x = k\pi \)
• Range: \( (-\infty, -1] \cup [1, \infty) \)
• Period: \( 2\pi \)
• Symmetry: Since \( \csc(-x) = -\csc x \), cosecant is an odd function.
• Vertical asymptotes: \( x = k\pi \)

More resources: Trigonometric Functions Overview