Vectores en 3D (R³): Guía Completa y Operaciones

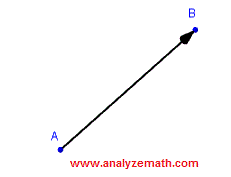
¿Qué es un vector?

Un vector es una cantidad que tiene tanto una magnitud como una dirección. Se representa geométricamente mediante un segmento de línea cuya longitud es la magnitud y una flecha que indica su dirección, como se muestra en la figura de abajo. Los vectores se utilizan en física para modelar cantidades con tamaños y direcciones, como velocidades, fuerzas, aceleraciones; y en ingeniería, química, gráficos por computadora, robótica y muchos otros campos.

En la figura de arriba, el vector se define usando un punto inicial A y un punto terminal B. Por lo tanto, el vector puede denotarse como \( \vec{AB} \).

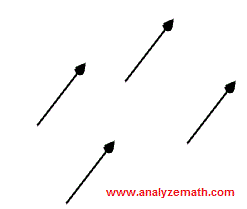
Vectores Equivalentes

Los vectores con magnitudes iguales y la misma dirección son vectores equivalentes, independientemente de su posición en el espacio.

Operaciones Vectoriales Geométricas

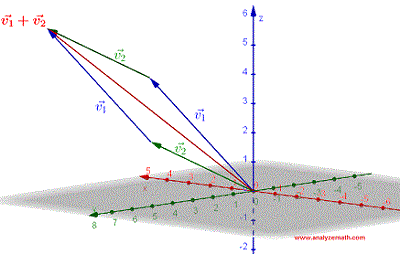
Suma de dos vectores

Dados dos vectores \( \vec{v_1} \) y \( \vec{v_2} \), su suma es un vector que se obtiene colocando primero el vector \( \vec{v_2} \) de tal manera que su punto inicial coincida con el punto terminal de \( \vec{v_1} \). La suma \( \vec{v_1} + \vec{v_2} \) es el vector cuyo punto inicial es el punto inicial de \( \vec{v_1} \) y su punto terminal es el punto terminal de \( \vec{v_2} \).

Observa que \( \vec{v_1} + \vec{v_2} = \vec{v_2} + \vec{v_1} \). Además, la suma de dos vectores coincide con la diagonal del paralelogramo determinado por \( \vec{v_1} \) y \( \vec{v_2} \).

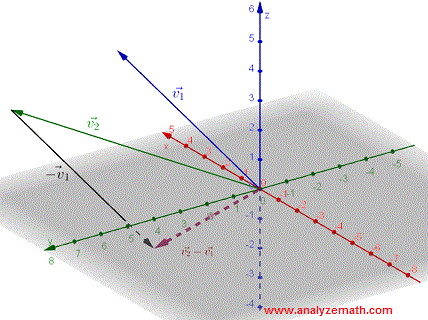
Diferencia de dos vectores

Dados dos vectores \( \vec{v_1} \) y \( \vec{v_2} \), la diferencia \( \vec{v_2} - \vec{v_1} \) puede definirse como la suma \( \vec{v_2} + (- \vec{v_1}) \) y representarse geométricamente como se muestra a continuación.

Multiplicación de un vector por un escalar

Un vector \( \vec{v_1} \) multiplicado por un escalar \( k \) se define como un vector \( k\vec{v_1} \) paralelo a \( \vec{v_1} \), cuya dirección es la misma que la de \( \vec{v_1} \) si \( k \gt 0 \) y opuesta si \( k \lt 0 \). La magnitud (longitud) de \( k\vec{v_1} \) es \( | k | \) veces la magnitud de \( \vec{v_1} \).

La figura de abajo muestra los vectores \( \vec{v_1} \), \( 2\vec{v_1} \) y \( -3 \vec{v_1} \).

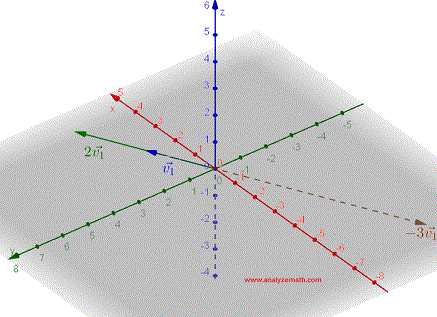
Vectores en un Sistema de Coordenadas Rectangulares 3D

Un vector unitario es un vector con una magnitud igual a 1. A continuación se muestra un sistema de coordenadas rectangulares en 3D con vectores unitarios \(\vec{i} \), \(\vec{j} \) y \(\vec{k} \) en la dirección positiva de los ejes x, y y z respectivamente. Los vectores \(\vec{i} \), \(\vec{j} \) y \(\vec{k} \) pueden definirse por sus componentes de la siguiente manera:

• \(\vec{i} = \langle 1 , 0 , 0 \rangle\), una unidad a lo largo del eje x.
• \(\vec{j} = \langle 0 , 1 , 0 \rangle\), una unidad a lo largo del eje y.
• \(\vec{k} = \langle 0 , 0 , 1 \rangle\), una unidad a lo largo del eje z.

Componentes de un vector

Los componentes de cualquier vector \(\vec{v} \) se definen expresando \(\vec{v} \) como una suma de múltiplos de los vectores unitarios \(\vec{i} \), \(\vec{j} \) y \(\vec{k} \) de la siguiente manera:

O en forma de componentes usando corchetes angulares como sigue:

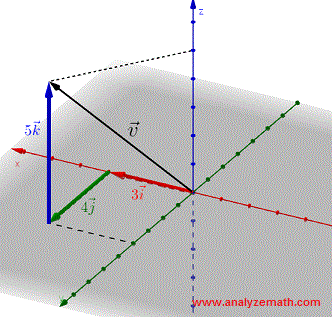
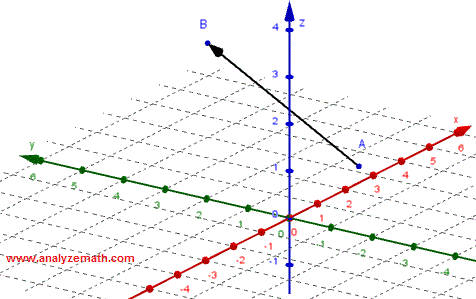
Los componentes de un vector \(\vec{v} \) definido por su punto inicial \( A = (x_1 , y_1 , z_1) \) y su punto terminal \( B = (x_2 , y_2 , z_2) \) vienen dados por:

Cálculo de Magnitud y Vectores Unitarios

Dado el vector \( \vec{v} = \langle a, b, c \rangle \), su magnitud (o longitud) viene dada por:

El vector unitario \( \vec{u} \), definido como un vector de magnitud igual a 1, en la misma dirección que \( \vec{v} \), viene dado por:

Suma, Diferencia y Multiplicación Escalar Algebraica

Dados los vectores \( \vec{v_1} = \langle a_1, b_1, c_1 \rangle \) y \( \vec{v_2} = \langle a_2, b_2, c_2 \rangle \), la suma \( \vec{v_1} + \vec{v_2} \), la diferencia \( \vec{v_1} - \vec{v_2} \), y la multiplicación escalar \( k \vec{v_1} \) (donde k es un número real) vienen dadas por: