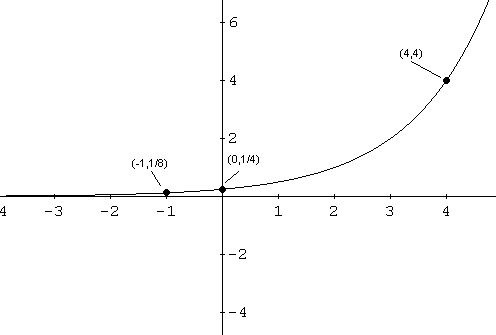Gráficas de Funciones Exponenciales

Graficar y trazar funciones exponenciales: tutorial paso a paso. Se analizan en detalle propiedades como el dominio, el rango, las asíntotas horizontales y los interceptos de las gráficas de estas funciones. También está disponible papel cuadriculado gratuito.

Repaso

Comenzamos con las propiedades de la gráfica de la función exponencial básica definida por:

De base \( a \),

\[ f(x) = a^x , \quad a \ge 0 \quad \text{y} \quad a \ne 1. \]

El dominio de la función \( f \) es el conjunto de todos los números reales. El rango de \( f \) es el intervalo \( (0 , +\infty) \).

La gráfica de \( f \) tiene una asíntota horizontal dada por \( y = 0 \). La función \( f \) tiene un intercepto con el eje \( y \) en \( (0 , 1) \).

La función exponencial \( f \) es creciente si \( a > 1 \) y decreciente si \( a < 1 \).

Ejemplo 1

La función \( f \) está dada por

\[ f(x) = 2^{x - 2} \]
  1. Encuentre el dominio y el rango de \( f \).
  2. Encuentre la asíntota horizontal de la gráfica.
  3. Encuentre los interceptos con los ejes \( x \) e \( y \), si existen.
  4. Trace la gráfica de \( f \).

Respuesta al Ejemplo 1

  1. El dominio de \( f \) es el conjunto de todos los números reales.

    Para encontrar el rango de \( f \), comenzamos con \[ 2^x > 0 \] Multiplicamos ambos lados por \( 2^{-2} \), que es un número positivo: \[ 2^x \cdot 2^{-2} > 0 \] Usando propiedades de los exponentes: \[ 2^{x-2} > 0 \] Esto indica que \( f(x) > 0 \). Por lo tanto, el rango de \( f \) es: \[ (0, +\infty) \]
  2. Cuando \( x \) disminuye sin límite (\( -\infty \)), \( f(x) = 2^{x-2} \) se aproxima a \( 0 \). Por lo tanto, la gráfica de \( f \) tiene una asíntota horizontal en \( y = 0 \).
  3. Para encontrar el intercepto con el eje \( x \), resolvemos \[ f(x) = 0 \] \[ 2^{x-2} = 0 \] Como \( f(x) > 0 \), esta ecuación no tiene solución. La gráfica no tiene intercepto con el eje \( x \).

    El intercepto con el eje \( y \) es: \[ (0 , f(0)) = (0 , 2^{-2}) = \left(0 , \frac{1}{4}\right) \]
  4. Ya conocemos el dominio, el rango, el intercepto con \( y \) y la asíntota horizontal. Necesitamos algunos puntos adicionales.
    5. \[ (4 , f(4)) = (4 , 2^{4-2}) = (4 , 4) \] \[ (-1 , f(-1)) = (-1 , 2^{-3}) = \left(-1 , \frac{1}{8}\right) \]

    Ahora utilizamos toda esta información para graficar \( f \).

    Gráfica de función exponencial

Problema Similar al Ejemplo 1

La función \( f \) está dada por:

\[ f(x) = 2^{x + 2} \]
  1. Encuentre el dominio y el rango de \( f \).
  2. Encuentre la asíntota horizontal.
  3. Encuentre los interceptos con los ejes, si existen.
  4. Trace la gráfica.

Ejemplo 2

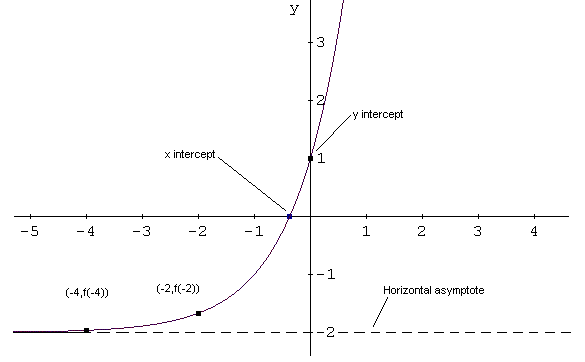
Sea \( f \) la función definida por:

\[ f(x) = 3^{x+1} - 2 \]

Respuesta al Ejemplo 2

  1. El dominio de \( f \) es el conjunto de todos los números reales.

    Partimos de: \[ 3^x > 0 \] Multiplicamos por \( 3 \): \[ 3^{x+1} > 0 \] Restamos 2: \[ 3^{x+1} - 2 > -2 \] Esto indica que \( f(x) > -2 \). Por lo tanto, el rango es: \[ (-2, +\infty) \]
  2. Cuando \( x \to -\infty \), \( 3^{x+1} \to 0 \) y \( f(x) \to -2 \). La asíntota horizontal es \( y = -2 \).
  3. Para el intercepto con \( x \): \[ 3^{x+1} - 2 = 0 \] \[ 3^{x+1} = 2 \] \[ x + 1 = \log_3(2) \] \[ x = \log_3(2) - 1 \] El intercepto con \( y \) es: \[ (0 , f(0)) = (0 , 1) \]
  4. Usamos esta información para trazar la gráfica.

    5. Gráfica de función exponencial con traslación

Problema Similar al Ejemplo 2

\[ f(x) = 2^{x - 2} + 1 \]
  1. Encuentre el dominio y el rango.
  2. Determine la asíntota horizontal.
  3. Encuentre los interceptos.
  4. Trace la gráfica.

Más Referencias y Enlaces