Percent Math Questions

Several questions on percentages with detailed solutions are presented below.

Question 1

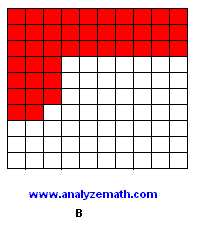
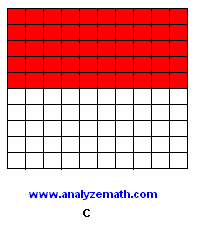
What percentage of the large square is coloured red in each figure below?

Solution to Question 1

In figure A, 1 small square out of a total of 100 is colored red, so we have:
\[ \frac{1}{100} = 1\% \] In figure B, 41 small squares out of 100 are colored red:
\[ \frac{41}{100} = 41\% \] In figure C, 50 small squares out of 100 are colored red:
\[ \frac{50}{100} = 50\% = \frac{1}{2} \] In figure D, all 100 small squares are red:
\[ \frac{100}{100} = 100\% = 1 \]

Question 2

What percent of the balls in the figure below are red?

Solution to Question 2

5 balls out of a total of 9 are red, so in fraction form we have:
\[ \frac{5}{9} \] Divide 5 by 9 to obtain the decimal:
\[ \frac{5}{9} \approx 0.56 \] Convert to percentage:
\[ 0.56 \times 100 = 56\% \] Approximately 56% of the balls are red.

Question 3

What is 12% of 250?

Solution to Question 3

Let the unknown be \(y\). The word "of" represents multiplication and "is" represents equality. Mathematically:
\[ y = 12\% \times 250 \] Rewrite the percentage as a fraction:
\[ y = \frac{12}{100} \times 250 = \frac{12 \cdot 250}{100} = 30 \] Hence, 12% of 250 is 30.

Question 4

4 is what percent of 32?

Solution to Question 4

Let the unknown percent be \(y\%\). Then:
\[ 4 = y\% \times 32 \] Solve for \(y\%\):
\[ y\% = \frac{4}{32} = 0.125 \] Convert to percentage:
\[ y\% = 0.125 \times 100 = 12.5\% \] Check: 12.5% of 32 is 4.

Question 5

6 is 80% of what number?

Solution to Question 5

Let \(x\) be the unknown number:
\[ 6 = 80\% \times x \] Rewrite 80% as fraction:
\[ x = \frac{6}{\frac{80}{100}} = 6 \cdot \frac{100}{80} = \frac{600}{80} = 7.5 \] Check: 80% of 7.5 is 6.

Question 6

A number increased from 120 to 150. By what percent of its original value did this number increase?

Solution to Question 6

The part is the increase:
\[ \text{part} = 150 - 120 = 30 \] The whole is 120, hence the percent:
\[ x = \frac{\text{part}}{\text{whole}} = \frac{30}{120} = 0.25 \] Convert to percentage:
\[ x = 0.25 \times 100 = 25\% \] Hence, the number increased by 25%.

Question 7

A number decreased from 80 to 50. By what percent of its original value has this number decreased?

Solution to Question 7

The part is the decrease:
\[ \text{part} = 80 - 50 = 30 \] The whole is 80, hence the percent:
\[ x = \frac{\text{part}}{\text{whole}} = \frac{30}{80} = 0.375 \] Convert to percentage:
\[ x = 0.375 \times 100 = 37.5\% \] Hence, the number decreased by 37.5%.

Question 8

Which is greater: 15% of 380 or 25% of 210?

Solution to Question 8

Let \(x = 15\% \text{ of } 380\):
\[ x = \frac{15}{100} \cdot 380 = 57 \] Let \(y = 25\% \text{ of } 210\):
\[ y = \frac{25}{100} \cdot 210 = 52.5 \] Hence, 15% of 380 is greater than 25% of 210.