Find The Focus of Parabolic Dish Antennas
The position of the focus (of a parabolic dish antenna or parabolic reflector) is found in term of the diameter of the dish and its depth.
Focus of a Parabola
We first write the equations of the parabola so that the focal distance (distance from vertex to focus) appears in the equation.The figure below shows a parabola, its focus F at (0,f) and its directrix at y = -f.
We now use the definition of the parabola . Any point M(x,y) on the parabola is equidistant from the focus and the directrix. Hence the equation:
√[(x-0) 2 + (y - f) 2 ] = √[(x - x) 2 + (y - (-f)) 2 ]
We now square both sides and expand the squares.
x 2 + y 2 + f 2 - 2y*f = y 2 + f 2 + 2y*f
Simplify to obtain the equation of the parabola involving the focal distance f.
We now look at a more practical situation where we know the dimensions of the dish and we want to find the focal distance which gives the position of the focus relative to the position of the dish as swown in the figure below.
D is the diameter of the dish, d is the depth of the dish and f is the focal distance.
The points (D/2,d) and (-D/2,d) are on the parabola, hence
d = (D/2) 2 / 4f
Which gives a relationship between the diameter D, the depth d and the focal distance f of the dish.
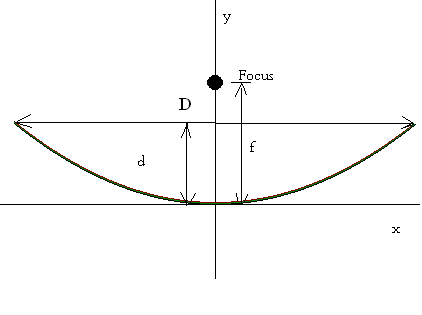
The above formula helps in positioning the feed of the parabolic antennas as it gives the focal distance f. Of course in practice the shape of the dish is not a perfect parabola and therefore small adjustments are needed when positioning the feed.
A focus of parabolic reflector calculator is included in this site.
Exercises
1 - Find the focal distance f for a dish that has a diameter D = 80 cm and a depth d = 25 cm.2 - Find a relationship between the diameter D and the depth d so that the focal distance f is equal to twice the depth d of the parabolic dish.
3 - Find a relationship between the diameter D and the depth d so that the focal distance f is greater than d.
More References and Links to Parabolic Reflector and Antennas
Tutorial on How Parabolic Dish Antennas work?Interactive tutorial on Parabolic Reflectors and Antennas work.
Dipole Antennas
Antenna Polarization
Antenna Arrays
Interactive tutorial on the Equation of a Parabola .
Interactive tutorial on how to find the equation of a parabola .
Define and Construct a Parabola .
