Euler Constant e
In compounding of interest it was shown that if, for example, an amount of money P (principal) is invested at an annual percentage rate r, the total amount of money A after t years is given byA=P(1+r)t
It was also shown that if the interest is compounded n times during each year, the amount of money after t years is given by
A=P(1+r/n)nt
Let N=n/r , then r/n=1/N and n=rN , hence the formula for A becomes
A=P(1+1/N)Nrt
Which can be written as
A=P((1+1/N)N)rt
The question that one may ask is that what if we increase n indefinitely?
As the number of compounding n increases, N also increases, the term (1+1/N)N approaches a constant value called e (after the swiss mathematician Leonhard Euler) and is approximately equal 2.718282....
The table of values below shows the values of (1+1/N)N as N increases.
| N | (1+1/N)N |
| 1 | 2 |
| 2 | 2.25 |
| 3 | 2.37037 |
| 10 | 2.59374 |
| 20 | 2.65329 |
| 40 | 2.68506 |
| 100 | 2.70481 |
| 200 | 2.71149 |
| 400 | 2.71488 |
Below is shown the graph of y=(1+1N)N as a function of N and we can see that as N increases, y=(1+1N)N approaches a constant e≈2.71828182846
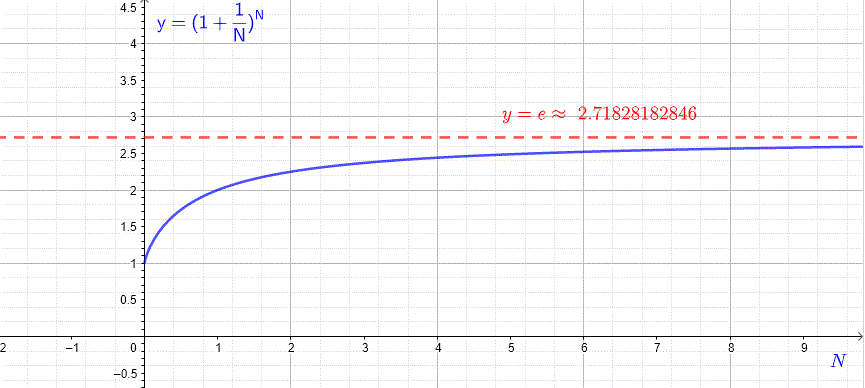
More rigorously, e is defined as the limit of (1+1/N)N as N approaches infinity which is written as
e=limN→∞(1+1N)N Let m=1N and rewrite another definition of the Euler constant e as follows
e=limm→0(1+m)1m
The continuous compounding is defined for N very large and in this case the amount of money after t years is given by
A=Pert
Exponential and Logarithmic Functions to the Base e
The Euler constant e defined above plays an important role in applied mathematics. Many mathematical models used in physics, engineering, chemistry, economics,..., are described by exponential functions to the base e defined by
f(x)=ex
and it inverse, the logarithm to the base e, defined by
g(x)=ln(x)
Fundtion f is called the natural exponential function and the function g is called the natural logarithmic function. Both are graphed below.
