Find the derivatives of various functions using different methods and rules in calculus. Several Examples with detailed solutions are presented. More exercises with answers are at the end of this page.

Example 1: Find the derivative of function f given by Solution to Example 1:
Function f is the product of two functions: U = x ² - 5 and V = x ³ - 2 x + 3; hence We use the product rule to differentiate f as follows: where U ' and V ' are the derivatives of U and V respectively and are given by Substitute to obtain Expand, group and simplify to obtain

Example 2: Calculate the first derivative of function f given by
\[ f(x) = (\sqrt x + 2x)(4x^2-1) \]
Solution to Example 2:
This function may be considered as the product of function U = √x + 2x and V = 4x² - 1, hence the use of the product rule
\[ f'(x) = U' V + U V' \\ = (\dfrac{1}{2\sqrt x} + 2)(4x^2-1) + (\sqrt x + 2 x)(8x) \] To add the above you need to write all terms as fractions with a common denominator.
\[ f'(x) = \dfrac{(1+2\cdot2\sqrt x)(4x^2-1)+2\sqrt x(8x)(\sqrt x + 2x)}{2\sqrt x} \] Expand
\[ f'(x) = \dfrac{4x^2-1+16x^{5/2}-4\sqrt x+16x^2+32x^{5/2}}{2\sqrt x} \] and group to obtain the final result for the derivative of f as follows.
\[ f'(x) = \dfrac{48x^{5/2}+20x^2-4x^{1/2}-1}{2\sqrt x} \]

Example 3: Calculate the first derivative of function f given by

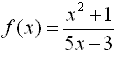
Solution to Example 3:
The given function may be considered as the ratio of two functions: U = x² + 1 and V = 5x - 3 and use the quotient rule to differentiate f is used as follows
Expand and group to obtain f'(x) as follows

Example 4: Calculate the first derivative of function f given by

Solution to Example 4:
Function f is the quotient of two functions hence the use of the quotient rule
Write all terms in the numerator so that they have the same denominator 2 sqrt x
Expand and group like terms to obtain f'(x)

Example 5: Calculate the first derivative of function f given by

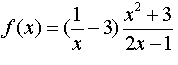
Solution to Example 5:
Function f given above may be considered as the product of functions U = 1/x - 3 and V = (x² + 3)/(2x - 1), and function V may be considered as the quotient of two functions x² + 3 and 2x - 1. We use the product rule for f and the quotient rule for V as follows
Set all terms to a common denominator
Expand and group to obtain the derivative f'.

Example 6: Calculate the first derivative of function f given by

Solution to Example 6:
There are several ways to find the derivative of function f given above. One of them is to consider function f as the product of function U = sqrt x and V = (2x - 1)(x³ - x) and also consider V as the product of (2x - 1) and (x³ - x) and apply the product rule to f and V as follows
Set a common denominator to all terms
Expand and group like terms to obtain the derivative f'.

Example 7: Find the derivative of function f given by

Solution to Example 7:
The given function is of the form U⁴ where U = x³ + 4. The use of the chain rule of differentiation gives f ' as follows
Calculate U ' and substitute above to obtain f ' as follows

Example 8: Find the derivative of function f given by

Solution to Example 8:
Function f is of the form U³ where U = (x - 1) / (x + 3). Apply the chain rule to obtain f ' as follows
Calculate U ', using the quotient rule, and substitute to obtain
Expand and group like terms to obtain a final form for the derivative f '

Example 9: Find the derivative of function f given by

Solution to Example 9:
The given function is of the form sqrt U with U = x³ + 2 x + 1. Calculate U ' and use the chain rule to obtain

Example 10: Find the derivative of function f given by

Solution to Example 10:
The given function is of the form U^3/2 with U = x² + 5. Apply the chain rule as follows
Calculate U ', substitute and simplify to obtain the derivative f '.

Example 11: Find the derivative of function f given by

Solution to Example 11:
Function f is of the form U^1/4 with U = (x + 6)/(x + 5). Use the chain rule to calculate f ' as follows
Since U is the quotient of two function, use the quotient rule to find U ' and substitute to obtain
Expand and group like terms
Change the negative exponent into a positive exponent to find a final form of f ' as follows

Exercises: Find the derivative of each of the following functions.

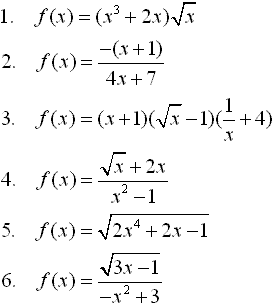
Answers to Above Exercises: