Examples with Detailed Solutions
Example 1
a) Factor polynomial P given byP (x) = - x3 - x2 + 2x
b) Determine the multiplicity of each zero of P.
c) Determine the sign chart of P.
d) Graph polynomial P and label the x and y intercepts on the graph obtained. Solution to Example 1
-
a) Factor P as follows
P (x) = - x3 - x2 + 2x
= - x (x2 + x - 2)
= - x (x + 2)(x - 1)
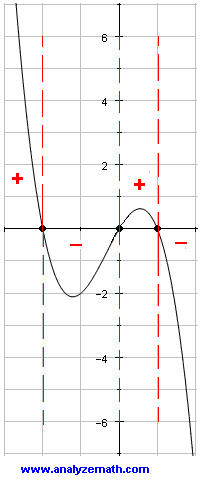
b) P has three zeros which are -2, 0 and 1 and are all of multiplicity one.
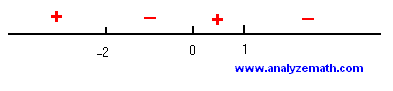
c) The three zeros of P will split the number line into four intervals given by:
(- ? , -2) , (- 2 , 0) , (0 , 1) and (1 , +?)
select one value of x within each interval and evaluate polynomial P for this value to determine the sign of P.
P(-3) = 12 > 0 , P(-1) = - 2 < 0 , P(1/2) = 5/8 >0 , P(2) = - 8 < 0
Using the signs of P with each interval, the sign chart is as follows:
Example 2
a) Factor polynomial P given byP (x) = x4 - 2 x2 + 1
b) What is the multiplicity of each zero of P?
c) Determine the sign chart of P.
d) Graph polynomial P and label the x and y intercepts on the graph obtained.
e) What is the range of polynomial P? Solution to Example 2
- a) Factor P as follows
P (x) = x4 - 2 x2 + 1
= (x2 - 1)2
= ((x - 1)(x + 1))2
= (x - 1)2 (x + 1)2
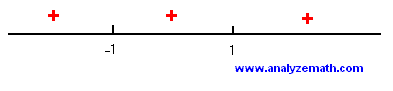
- b) Polynomial P has zeros at x = 1 and x = -1 and both has multiplicity 2.
- c) Polynomial P(x) is a perfect square and therefore positive or zero for all real values of x. P(x) is equal to zero at the two zeros -1 and 1 and positive everywhere else. The sign chart is as follows:
- d) The x intercepts are at (-1,0) and (1,0) and the y intercept is at (0,1). The graph of P touches the x axis at x = -1 and x = 1 and opens up since P(x) is positive, cutting the y axis at (0,1). See graph below.
- e) Using the graph of P above, the range of P is given by the interval
[ 0 , + ?)
Example 3
a) Show that x = - 3 is a zero of polynomial P given byP (x) = x4 + 5 x3 + 5 x2 - 5 x - 6
b) Show that (x - 1) is a factor of P.
c) Factor P and determine the multiplicity of each zero of P.
d) Determine the sign chart of P.
e) Graph polynomial P and label the x and y intercepts on the graph obtained. Solution to Example 3
- a) Calculate P(-3)
P (-3) = (-3)4 + 5 (-3)3 + 5 (-3)2 - 5 (-3) - 6
= 0
Hence -3 is a zero of P and x + 3 is a factor of P(x).
- b) Since (x + 3) is a factor of P(x), the division of P(x) by (x + 3) must give a remainder equal to zero. Hence
P(x) / (x + 3) = x3 + 2 x2 - x - 2
We now divide x3 + 2 x2 - x - 2 by (x - 1)
(x3 + 2 x2 - x - 2) / (x - 1) = x2 + 3x + 2 , remainder equal to zero which proves that (x - 1) is a factor of x3 + 2 x2 - x - 2 and therefore of P(x).
- c) Using the above, P(x) may be written as follows
P(x) = (x + 3)(x - 1)(x2 + 3x + 2)
We now factor the quadratic term x2 + 3x + 2 included in P(x). Hence
P(x) = (x + 3)(x - 1)(x + 1)(x + 2)
P has zeros at x = -3, -2, -1 and 1 and are all of multiplicity one.
- d) The sign chart is shown below
- e) Using the information on the zeros and the sign chart, the graph of P is as shown below with x and y intercepts labeled.
Example 4
x = 1 is a zero of multiplicity 2 of polynomial P defined byConstruct a sign chart for P and graph it. Solution to Example 4
- If x = 1 is a zero of multiplicity 2, then (x - 1)2 is a factor of P(x) and a division of P(x) by (x - 1)2 yields a remainder equal to 0. Hence
P (x) / (x - 1)2
= (x5 + x4 - 3 x3 - x2 + 2 x) / (x - 1)2
= x3 + 3 x 2 + 2 x
P(x) is now factored as follows
P(x) = (x - 1)2 (x3 + 3 x 2 + 2 x)
= x (x - 1)2 (x2 + 3 x + 2 )
= x (x - 1)2 (x + 1)(x + 2)
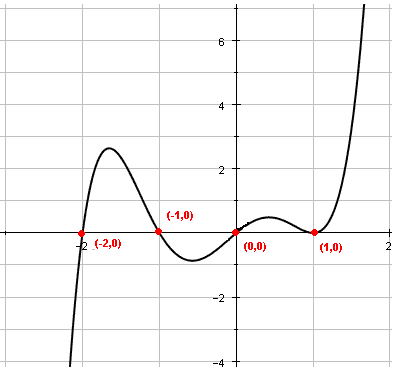
P(x) has 4 zeros at x = -2, -1, 0 and 1 and the zero at x= 1 is of multiplicity 2.
The sign chart is shown below
Use the sign chart and the zeros of P to grpah P as shown below.
