Find Equation of a Circle From a Graph

Examples with Detailed Solutions

Example 1
Find the equation of the circle whose graph is shown below.




Solution to Example 1
The given graph is symmetric with respect to the x-axis and therefore the center of the circle is the midpoint of the two x intercepts at the points \( (-1,0) \) and \( (3,0) \). In other words the two x intercepts form a diameter of the circle. Hence the center of the circle is at their midpoint given by
\( (\dfrac{-1+3}{2} , \dfrac{0+0}{2} ) = (1,0) \)
The radius \( r \) of the circle is half the diameter. Hence
\( r = \dfrac{1}{2} \sqrt{(-1-3)^2 +(0 - 0)^2} = 2\)
The equation of the circle whose graph is given above is
\( (x - 1)^2 + y^2 = 2^2\)

Example 2
Find the equation of the circle whose graph is shown below.




Solution to Example 2
We first draw two perpendicular axes of symmetry (broken lines) of the circle in order to locate the center of the circle.





From the above graph with the axes of symmetry, we can approximate the center to be at the point \( (1,-2) \)
The points of intersection of the circle with any of the two axes (broken lines) give a diameter of about \( 6 \) units and therefore the radius is half the diameter which is 3 units.
The equation of the circle whose graph is given above is
\( (x - 1)^2 + (y + 2)^2 = 3^2\)

Example 3
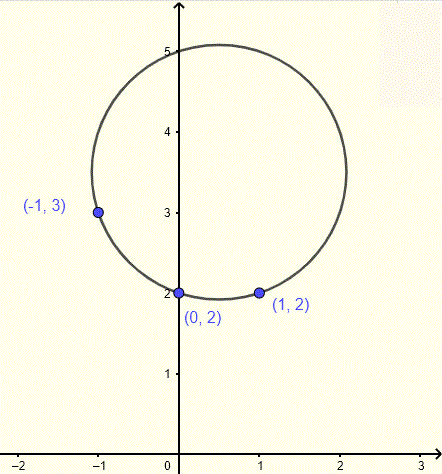
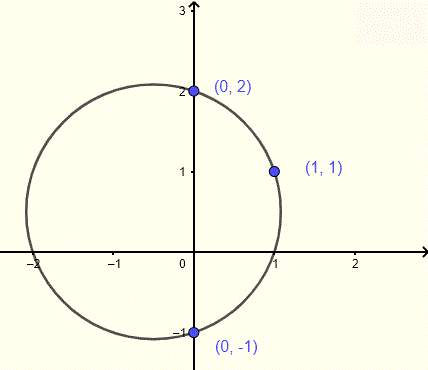
Find the equation of the circle whose graph is shown below including three points on the circle.




Solution to Example 3
Let \( (h , k) \) be the center of the circle. Three points \( (-1,3) \), \( (0,2) \) and \( (1,2) \) are on the graph of the circle and therefore the distance from each point to the center is equal to the radius. To avoid square roots, with equate the square of the distances from the center to each of the given points.
The square of the distance from the center \( (h , k) \) to the point \( (-1,3) \) is given by
\( (h + 1)^2 + (k - 3)^2 \)
The square of distance from the center other to the point \( (0,2) \) is given by
\( (h - 0)^2 + (k - 2)^2 \)
The square of distance from the center other to the point \( (1,2) \) is given by
\( (h - 1)^2 + (k - 2)^2 \)
All three distances are equal and we therefore deduce the equations
\( (h + 1)^2 + (k - 3)^2 = h^2 + (k - 2)^2 \) and \( h^2 + (k - 2)^2 = (h - 1)^2 + (k - 2)^2\)
Because of the the term \( (k - 2)^2 \) in the the second equations, the latter may be simplified to
\( h^2 = (h - 1)^2 \)
Expand the right hand side and simplify to obtain
\( 0 = -2 h + 1 \)
Solve for h
\( h = \dfrac{1}{2} \)
Substitute \( h \) by \( \dfrac{1}{2} \) in the equation \( (h + 1)^2 + (k - 3)^2 = h^2 + (k - 2)^2 \)
\( (\dfrac{1}{2} + 1)^2 + (k - 3)^2 = (\dfrac{1}{2})^2 + (k - 2)^2 \)
Expand the above and group like terms to obtain
\( k^2-6k+\frac{45}{4} = k^2-4k+\frac{17}{4} \)
Solve the above to obtain
\( k=\frac{7}{2} \)
The radius \( r \) is given by the distance from the center at \( (h,k) = (\dfrac{1}{2},\dfrac{7}{2}) \) to any of the three points. Let us use the point \( (0,2) \) to find r as follows
\( r = \sqrt{ (\dfrac{1}{2} - 0)^2 + (\frac{7}{2} - 2)^2 } = \sqrt{\dfrac{5}{2}}\)
We now have the center at \( (\dfrac{1}{2} ,\frac{7}{2})\) and the radius \( r = \sqrt{\dfrac{5}{2}} \) and therefore the equation of the circle is given by
\( \left(x - \dfrac{1}{2} \right)^2 + \left(y - \dfrac{7}{2} \right)^2 = \dfrac{5}{2} \)
The three points circle calculator may be used to check answers and generate more problems to practice.

Exercises with Answers

Find the equation of the circle for each of the graphs below

1. \( (x - 3)^2 + y^2 = 4 \)
2. \( (x + 2)^2 + (y-1)^2 = 9 \)
3. \( \left(x+\dfrac{1}{2}\right)^2+ \left(y-\dfrac{1}{2} \right)^2= \dfrac{5}{2} \)

More References and links